BAC - QCM

F4 - Fonc/usuelles BAC - QCM Tale ES
Exercice 1(Antilles, Guyane Septembre 2013)
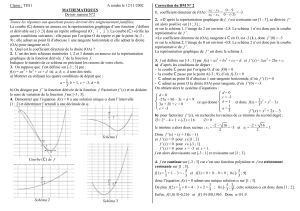
La courbe Cd’une fonction fdéfinie et dérivable sur Rest donnée ci-dessous. La
courbe Cpasse par les points A(−1 ; e) et B(0 ; 2) où e = exp(1).
La tangente à la courbe Cau point Aest horizontale et la tangente à la courbe C
au point Best la droite (BD), où Da pour coordonnées (2 ; 0).
1
2
3
4
-1
-2
-3
1 2 3-1-2-3 x
y
0
A
B
D
1. L’équation f(x) = 1 admet exactement trois solutions dans [−2 ; 3 ].
2. f′(−1) = 0.
3. f′(0) = −1.
4. f′(x)>0 sur l’intervalle [ 1 ; 3 ].
Exercice 2(France métropolitaine La Réunion Septembre 2013)
On considère une fonction fdéfinie sur l’intervalle [−1 ; 3 ], deux fois dérivable sur
cet intervalle et dont la représentation Cfdans un repère orthonormé est proposée
ci-dessous.
On désigne par f′la fonction dérivée de f, par f′′ la fonction dérivée seconde de f,
par Fune primitive de f(On admet l’existence de F).
La droite Dest tangente à Cfau point Ad’abscisse 1, seul point en lequel la courbe
traverse la tangente.
L’axe des abscisses est tangent à Cfau point d’abscisse 2.
La tangente à Cfau point d’abscisse 0 est la droite d’équation y= 4.
1
2
3
4
5
6
-1
1 2 3 4-1-2 0x
y
D
A
Cf
1. (a) f(1) = 5
(b) f′(1) = 2
(c) La tangente à Cfau point d’abscisse 1 a
pour équation y=−3x+ 5.
2. (a) f′(x)>0 pour tout xde l’intervalle
]−1 ; 2 [.
(b) f′est croissante sur l’intervalle ] 1 ; 2 [.
(c) f(x) = 0 si et seulement si x= 0 ou x= 2
(d) f′(x)60 pour tout xde l’intervalle
]−2 ; −1 [.
3. (a) f′est croissante sur l’intervalle ] −1 ; 2 [.
(b) f′(1) < f′(2).
(c) fest croissante sur l’intervalle ] −1 ; 2 [.
Exercice 3
1. La somme S= 1 + 2 + 22+ 23+···+ 230 est égale à :
(a) −1 + 231
(b) 1 −231
(c) −1 + 230
(d) 1 −230
2. L’équation −x3
3+x2+ 3x= 0 admet sur R:
(a) la solution −2
(b) trois solutions distinctes
(c) aucune solution
(d) une unique solution
3. Les nombres entiers nsolutions de l’inéquation 1
2n
<0,003 sont tous les
nombres entiers ntels que :
(a) n>8
(b) n>9
(c) n68
(d) n69
N.DAVAL - mathematiques.daval.free.fr 1/1 Lycée Georges Brassens