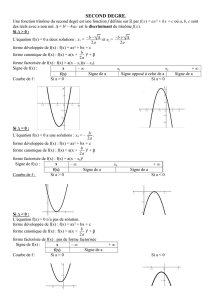
1 On considère la fonction homographique f telle que f(x) = 2 x – 3 x

1 On considère la fonction homographique f telle que f(x) = 2 x – 3
x – 1
a) Préciser l'ensemble de définition de la fonction f.
Vérifier que, pour tout réel x de D , on a : f(x) = 2 – 1
x –1
b) Etudier la fonction f . Préciser la transformation utilisée et la nature de la courbe C f .
2 Soit la fonction f telle que f(x) = x + 5
x + 2
a) Préciser l'ensemble de définition D de f . Calculer les images de 0 et de – 1 par f .
b) Trouver les réels a et b tels que f(x) = a + b
x + 2
b) Etudier la fonction f . Vérifier que la courbe C f est la translatée de la courbe d'équation y = 3
x par la translation
de vecteur – 2
→
i +
→
j .
3 On connaît le tableau des variations d'une fonction u, avec u(0) = 1 et u(2)
=0.
1° Tracer la courbe possible d'une telle fonction.
2° Dresser le tableau des variations de chacune fonctions données par :
a) f(x) = – 2 u(x) + 1 b) g(x) = – u(x – 3) – 2
c) h(x) = | u(x) | – 2 .
x – 3 – 1 5
f(x)
0
2
– 1
On précisera les valeurs aux bornes et les extrêmes.
4 On considère la fonction f donnée par : f(x) = – 2 x2 – 4 x + 6.
a) Exprimer f(x) – 8 en fonction de x . En déduire que l'on peut écrire : f(x) = a (x + α)2 + β.
b) Etudier le sens de variation de f, en précisant les tram formations qui permettent de passer de la parabole
d'équation y= 2 x2 à la courbe de la fonction f.
c) Résoudre l'équation f(x) = 6 , l'inéquation f(x) < 0 et l'inéquation f(x) ≥ 9 .
5 Soit f la fonction définie sur ] – 1 ; + ∞ [ p f(x) = 3 – 2
x + 1 et C f sa courbe représentative,
1° a) Calculer f(0) et f(– 1) .
b) Résoudre l'équation f(x) = 0 . En donner une interprétation graphique.
2° a) Etudier le sens de variation de la fonction f , en précisant la translation permettant de passer de l'hyperbole
de la fonction inverse à la courbe C f .
b) Tracer la courbe C f dans un repère orthonormé d'unité 1 cm en notant les points obtenus en 1°.
c) Tracer la droite d'équation y = x . En déduire 1 nombre de solutions de l'équation f(x) = x .
6 On considère les fonctions telles que : u(x) = (x – 3)2 – 9 ; f(x) = 1
x2 – 6 x et g(x) = 6x – x2.
a) Dresser le tableau des variations de la fonction u en indiquant son signe suivant les valeurs de x .
Développer u(x) .
b) Justifier que f est définie sur IR – { 0 ; 6 }. Dresser le tableau des variations de f .
c) Justifier que g est définie sur [ 0 ; 6 ] . Déterminer le sens de variation de la fonction g.
7 Sur le graphique ci-dessous sont représentées courbes C f et C g de
deux fonctions f et g définies sur IR
1° Déterminer le tableau des variations de 1
f et de 1 g
2° Déterminer le tableau des variations de f2 et g2
3° Déterminer le tableau des variations 2 f(x) – 3 et 1 – 2 g(x).

1 On considère la fonction homographique f telle que f(x) = 2 x – 3
x – 1
a) Préciser l'ensemble de définition de la fonction f. Vérifier que, pour tout réel x de D
D D
D , on a : f(x) = 2 – 1
x –1
2 – 1
x – 1 = 2 (x – 1) x – 1 – 1 x – 1 = 2 x – 2 – 1 x – 1 = 2 x – 3 x – 1 = f(x).
b) Etudier la fonction f . Préciser la transformation utilisée et la nature de la courbe C
CC
C f .
x
→
x – 1
→
1
x – 1
→
– 1
x – 1
→
2 – 1
x – 1
u : x
→
x – 1
v : x
→
1
x
w : x
→
2 – x
Sur ] 1 ; + ∞ [
la fonction u est croissante puis la fonction v est décroissante
enfin la fonction w est décroissante donc f est croissante
Sur ] – ∞ ; 1 [
la fonction u est croissante puis la fonction v est décroissante
enfin la fonction w est décroissante donc f est croissante
0
1
C
CC
C
1
1
y
x
C
CC
C
2
C
CC
C
3
C
CC
C
4
C2 , la courbe d'équation y = 1
x – 1 s'obtient à partir de C1 par translation de vecteur
→
i
C3 , la courbe d'équation y = – 1
x – 1 s'obtient à partir de C2 par symétrie autour de l'axe des abscisses.
C4 , la courbe d'équation y = 2 – 1
x – 1 s'obtient à partir de C2 par translation de vecteur 2
→
j
2 Soit la fonction f telle que f(x) = x + 5
x + 2 a) Préciser l'ensemble de définition D
D D
D de f . Calculer les images de 0 et de – 1 par f .
x + 2 ≠ 0 . Df = ] – ∞ ; – 2 [ union ; – 2 [ union ] – 2 ; + ∞ [
f(0) = 0 + 5
0 + 2 = 5 2 et f(– 1) = – 1 + 5 – 1 + 2 = 4
b) Trouver les réels a et b tels que f(x) = a + b
x + 2
a + b
x + 2 = a (x + 2) x + 2 + b x + 2 = a x + 2 a + b x + 2
Si on veut que a x + 2 a + b
x + 2 = x + 5 x + 2 il suffit de choisir a et b tels que a = 1 et 2 a + b = 5 c'est à dire a = 1 et b = 3
On a donc 1 + 3
x + 2 = x + 5 x + 2 variante x + 5 x + 2 = x + 2 + 3 x + 2 = x + 2 x + 2 + 3 x + 2 = 1 + 3 x + 2
C1 est la courbe d'équation y = 1
x

b) Etudier la fonction f. Vérifier que C
CC
C f est la translatée de la courbe d'équation y = 3
x par la translation de vecteur –2
→
→→
→
i +
→
→→
→
j .
x
→
x + 2
→
3
x + 2
→
1 + 3
x + 2
u : x
→
x + 2
v : x
→
3
x
w : x
→
1 + x
Sur ] – ∞ ; – 2 [ :
u est croissante puis v est décroissante et enfin w est croissante donc f est
décroissante.
Sur ] – 2 ; + ∞ [ :
u est croissante puis v est décroissante et enfin w est croissante donc f est
décroissante.
C1 est la courbe d'équation y = 3
x
C2 , la courbe d'équation y = 3
x + 2 s'obtient à partir de C1 par translation de vecteur – 2
→
i
C3 , la courbe d'équation y = 1 + 3
x + 2 s'obtient à partir de C2 par translation de vecteur
→
j
donc C3 , la courbe d'équation y = 1 + 3
x + 2 s'obtient à partir de C1 par translation de vecteur – 2
→
i +
→
j
0
1
1
y
x
C
CC
C
1
C
CC
C
3
C
CC
C
2
3 On connaît le tableau des variations d'une fonction u, avec u(0) = 1 et u(2) =0.
1° Tracer la courbe possible d'une telle fonction.
y
O
1
1
C
CC
C
h
C
CC
C
g
C
CC
C
u
C
CC
C
f
2° Dresser le tableau des variations de chacune fonctions données par :
a) f(x) = – 2 u(x) + 1 b) g(x) = – u(x – 3) – 2
c) h(x) = | u(x) | – 2 .
On précisera les valeurs aux bornes et les extrêmes.
x – 3 – 1 5
f(x)
0
2
– 1
a)
x – 3 – 1 5
f(x)
1
– 3
3
b)
x 0 2 8
f(x)
– 2
–4
– 1
c)
x – 3 – 1 2 5
f(x)
– 2
0
–2
– 1

4 On considère la fonction f donnée par : f(x) = – 2 x2 – 4 x + 6.
a) Exprimer f(x) – 8 en fonction de x . En déduire que l'on peut écrire : f(x) = a (x + α
αα
α)2 + β
ββ
β.
f(x) – 8 = – 2 x2 – 4 x + 6 – 8= – 2 x2 – 4 x – 2 = – 2 (x2 + 2 x + 1) = – 2 (x + 1)2
Donc f(x) = 8 – 2 (x + 1)2 et en posant : a = – 2, α = 1 et β = 8 on obtient l'égalité demandée.
b) Etudier le sens de variation de f, en précisant les tram formations qui permettent de passer de la parabole d'équation y= 2 x2 à
la courbe de la fonction f.
x
→
x + 1
→
2 (x + 1)2
→
– 2 (x + 1)2
→
– 2 (x + 1)2 + 8
t : x
→
x + 1
u : x
→
2 x2
v : x
→
– x
w : x
→
x + 8
• Sur ] – ∞ ; – 1 ] t est croissante, puis u est
décroissante, puis v est décroissante, enfin
w est croissante donc f est croissante
• Sur ] – 1 ; + ∞ ] t est croissante, puis u
est croissante, puis v est décroissante,
enfin w est croissante donc f est
décroissante
C1 est la courbe d'équation y = 2 x2
C2 , la courbe d'équation y = 2 (x + 1)2 s'obtient à partir de C1 par translation de vecteur –
→
i
C3 , la courbe d'équation y = – 2 (x + 1)2 s'obtient à partir de C2 par symétrie autour de l'axe des abscisses.
C4 , la courbe d'équation y = – 2 (x + 1)2 + 8 s'obtient à partir de C2 par translation de vecteur 8
→
j
c) Résoudre l'équation f(x) = 6 , l'inéquation f(x) < 0 et l'inéquation f(x) ≥
≥≥
≥ 9.
f(x) = 6 ⇔ – 2 (x + 1)2 + 8 = 6 ⇔ 8 – 6 = 2 (x + 1)2 ⇔ 2 (x + 1)2 = 2 ⇔ (x + 1)2 = 1 ⇔ x + 1 = 1 ou x + 1 = – 1
⇔ x = 0 ou x = – 2. S = { 0 ; – 2}
f(x) < 0 ⇔ 8 – 2 (x + 1)2 < 0 ⇔ 2 (22 – (x + 1)2) < 0
⇔ 2 (2 – (x + 1)) (2 + x + 1) < 0 ⇔ 2 (1 – x) (x + 3) < 0
x – ∞ – 3 1 + ∞
1 –x + + 0 –
x + 3 – 0 + +
f(x) – 0 + 0 –
5 Soit f la fonction définie sur ] – 1 ; + ∞
∞∞
∞ [ p f(x) = 3 – 2
x + 1 et C
CC
C f sa courbe représentative,
1° a) Calculer f(0) et f(– 1) .
f(0) = 3 – 2
0 + 1 = 3 – 2 = 1 f(– 1) n'existe pas
b) Résoudre l'équation f(x) = 0 . En donner une interprétation graphique.
f(x) = 0 ⇔ 3 – 2
x + 1 = 0 ⇔ 2 x + 1 = 3 ⇔ 2 = 3 (x + 1) ⇔ 3 x + 3 = 2 ⇔ x = – 1 3
– 1
3 est l'abscisse du point d'intersection de la courbe représentative de f, Cf avec l'axe des abscisses.
2° a) Etudier le sens de variation de la fonction f , en précisant la transformation permettant de passer de l'hyperbole de la
fonction inverse à la courbe C
CC
C f .
f : x
→
x + 1
→
2
x + 1
→
– 2
x + 1
→
3 – 2
x + 1
t : x
→
x + 1
u : x
→
2
x
v : x
→
– x
w : x
→
3 + x
Sur ] – ∞ ; – 1 [
t est croissante puis u est décroissante, puis v est
décroissante enfin w est croissante donc f est croissante
Sur ] – 1 ; + ∞ [
t est croissante puis u est décroissante, puis v est
décroissante enfin w est croissante donc f est croissante
C1 est la courbe d'équation y = 2
x
C2 , la courbe d'équation y = 2
x + 1 s'obtient à partir de C1 par translation de vecteur –
→
i
C3 , la courbe d'équation y = – 2
x + 1 s'obtient à partir de C2 par symétrie autour de l'axe des abscisses.
C4 , la courbe d'équation y = 3 – 2
x + 1 s'obtient à partir de C2 par translation de vecteur 3
→
j

b) Tracer la courbe C
CC
C f dans un repère orthonormé
d'unité 1 cm en notant les points obtenus en 1°.
c) Tracer la droite d'équation y = x .
En déduire 1 nombre de solutions de l'équation f(x) = x .
Il semble y avoir deux solutions
– 0,4 et 2,3
6 On considère les fonctions telles que : u(x) = (x – 3)2 – 9 ; f(x) =
1
x2 – 6 x et g(x) = 6x – x2. a) Dresser le tableau des variations de la
fonction u en indiquant son signe suivant les valeurs de x .
Développer u(x) .
u : x
→
x – 3
→
(x – 3)2
→
(x – 3)2 – 9
i : x
→
x – 3
j : x
→
x2
k : x
→
x – 9
Sur ] – ∞ ; 3 [ i est croissante, puis j décroissante et k est croissante
donc u est décroissante.
Sur ] 3 ; + ∞ [ i est croissante, puis j croissante et k est croissante
donc u est croissante.
u(x) = (x – 3)2 – 9 = x2 – 6 x + 9 – 9 = x2 – 6 x
b) Justifier que f est définie sur IR – { 0 ; 6 }. Dresser le tableau des variations de f.
v : x
→
1
x. u suivie de v donne la fonction f
Sur ] – ∞ ; 0 [, u est décroissante et v décroissante donc f est croisssante
Sur ] 0 ; 3 ] u est décroissante et v décroissante donc f est croisssante
Sur [ 3 ; 6 [ u est croissante et v décroissante donc f est décroisssante
Sur ] 6 ; + ∞ [ u est croissante et v décroissante donc f est décroisssante
c) Justifier que g est définie sur [ 0 ; 6 ].
Déterminer le sens de variation de la fonction g.
6 x – x2 = x (6 – x)
6 x – x2 ≥ 0 ⇔ x ∈ [ 0 , 6 ] donc Dg = [ 0 , 6 ]
w x
→
x. u suivie de w donne g
x –∞ 0 6 + ∞
x – 0 + +
6 – x + + 0 –
x2 – 6 x – 0 + 0 –
Sur ] 0 ; 3 ] u est décroissante et v croissante donc f est décroisssante
Sur [ 3 ; 6 [ u est croissante et v croissante donc f est croisssante
7 Sur le graphique ci-dessous sont représentées courbes C
CC
C f et C
CC
C g de deux fonctions f et g
définies sur IR 1° Déterminer le tableau des variations de 1
f et de 1 g
On suppose que f ne s'annule pas sur IR
x – ∞ 2 + ∞
f
2
x – ∞ 1,5 + ∞
1
f
1
2
x – ∞ 1,5 + ∞
g
0
x – ∞ 1,5 + ∞
g
2° Déterminer le tableau des variations de f2 et g2 3° Déterminer le tableau des variations 2 f(x) – 3 et 1 –
2 g(x).
x – ∞ 2 + ∞
f
2
x
–
∞
2 +
∞
f
2
4
x – ∞ 1,5 + ∞
g
0
x – ∞ 1,5 + ∞
g
2
0
x – ∞ 2 + ∞
2 f – 3
1
x
–
∞
1,5 +
∞
1
–
2 g
1
1
1
0
y
x