I Module et Argument d`un nombre complexe

TS Chapitre 10 : Les nombres complexes (2ème partie) 2012-2013
I Module et Argument d’un nombre complexe
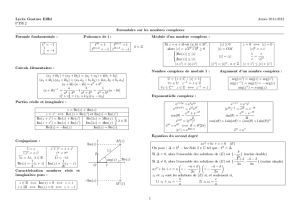
Tout point Mdu plan peut être repéré par un couple de coordonnées polaires
(r, θ) (r > 0, θréel)
•rest la distance OM ;
•θest une mesure de l’angle (~u, −−→ OM ).
Lien entre coordonnées cartésiennes et coordonnées polaires :
(r, θ) est un couple de coordonnées polaires de Met (x, y) les coordonnées
cartésiennes de M:
0~u
~v
M
r=OM
θ
On a : x=rcosθ et y=rsinθ ⇔r=px2+y2et cos(θ) = x
r,sin(θ) = y r.
I.1 Définition :
Définition 1 Soit zun nombre complexe non nul, Mle point d’affixe zet (r, θ)un couple de coordonnées polaires
de M. On décide des termes suivants :
•rest le module de zet cela se note r=|z|;
•θest un argument de zet cela se note θ=arg(z)[2π];
I.2 Propriétés :
•z=x+ iy, on a : |z|=px2+y2ou encore |z|2=x2+y2=zz
•Soit Md’affixe z, arg(z) = (−→ u;−−→ OM ) (2π)
•Pour tout réel x, le module de xest la valeur absolue de xet :
∗si x > 0, arg(x) = 0 (2π) ;
∗si x < 0, arg(x) = π2π) ;
•z6= 0, zimaginaire pur ⇔arg(z) = ±π
2(2π)
• |z|=|z|et arg(z) = −arg(z) (2π) ;
• | − z|=|z|et arg(−z) = π+arg(z) (2π) ;
Exemple 1 Calculer le module et l’argument de z1= 1 + i, z2= 1 + i√3,z3=−3iet z4= 2 + 3i
I.3 Forme trigonométrique d’un nombre complexe
Théorème 1 Tout nombre complexe znon nul peut s’écrire sous la forme
z=r(cosθ+ isinθ) où r=|z|et θ=arg(z) (2π).
Réciproquement : Si un nombre complexe non nul zs’écrit sous la forme z=r(cosθ + isinθ) avec r > 0 alors
|z|=ret arg(z) = θ(2π).
L’écriture z=r(cosθ + isinθ) s’appelle la forme trigonométrique de z.
My Maths Space 1 sur 5

TS Chapitre 10 : Les nombres complexes (2ème partie) 2012-2013
EXERCICE 1 1. Quelle est la forme trigonométrique de z1=−1 + i√3.
2. z2est un nombre complexe de module 3 et d’argument −π
4. Quelle est la forme algébrique de z2?
3. z3=−3(cos θ+ i sin θ). z3est-il écrit sous forme trigonométrique ?
Théorème 2 Soit z=r(cosθ + isinθ) et z′=r′(cosθ′+ isinθ′) deux nombres complexes. Alors, on a :
•zz′=rr′(cos(θ+θ′) + isin(θ+θ′)) ;
•z
z′=r r′(cos(θ−θ′) + isin(θ−θ′)) (z′6= 0) ;
Tableau récapitulatif des propriétés vérifiées par module et argument :
Quels que soient les nombres complexes zet z′(z′6= 0) :
P roduit |z×z′|=|z| × |z′|arg(zz′) =arg(z)+arg(z′) (2π)
P uissance |zn|=|z|narg(zn) = narg(z) (2π)
Inverse 
1
z
=1
|z|arg1 z=−arg(z) (2π)
Quotient 
z
z′
=|z|
|z′|argz z′=arg(z)−arg(z′) (2π)
Conjugu´e|z|=|z|arg(z) = −arg(z) (2π)
Oppos´e| − z|=|z|arg(−z) = π+arg(z) (2π)
Exemple 2 d’utilisation de la forme trigonométrique :
1. Calculer (1 + i√3)5;
2. Déterminer une forme trigonométrique de −√3 + i
−1−i.
3. Déterminer une forme trigonométrique de (√3 + 3i)(3 −i√3).
EXERCICE 2 On considère le nombre complexe :
z= 1 −√3 + i(1 + √3)
1. Écrire z2sous forme algébrique.
2. Déterminer le module et un argument de z2.
3. Indiquer le signe de la partie réelle de zet celui de la partie imaginaire, puis, à l’aide des propriétés sur module
et arguments, déterminer le module et un argument de z.
4. Déduire de ce qui précéde les lignes trigonométriques de 7π
12 , puis de π 12.
My Maths Space 2 sur 5

TS Chapitre 10 : Les nombres complexes (2ème partie) 2012-2013
II Notation Exponentielle
II.1 Notation
Si l’on pose f(θ) = cosθ + isinθ, le théorème 2 prouve que f(θ+θ′) = f(θ)×f(θ′)
De plus si l’on applique la formule de la dérivée d’une somme à la fonction f=cos + isin, on obtient : f′(θ) = if(θ),
d’où par analogie avec les relations vérifiées par l’exponentielle, on définit :
Définition : Pour tout réel θ, on pose eiθ=cosθ + isinθ
Conséquences :
•Tout nombre complexe znon nul, de module ret d’argument θs’écrit z=reiθ: cette écriture est appelée forme
exponentielle de zet réciproquement, de la même manière qu’avec la forme trigonométrique : si z=reiθet
r > 0, alors |z|=ret arg(z) = θ[2π].
•(important) |eiθ|= 1 et arg(eiθ) = θ[2π].
•Grâce aux propriétés des formes trigonométriques (th.2.) vues précédemment, l’exponentielle complexe possède
des propriétés qui rappellent celles de l’exponentielle réelle :
eiθ×eiθ′=ei(θ+θ′);eiθ
eiθ′=ei(θ−θ′);(eiθ)n=einθ ;eiθ=e−iθ.
EXERCICE 3 :
Écrire les nombres suivants sous forme algébrique : eiπ
6et 4eiπ 4.
Donner la forme exponentielle des nombres suivants : 1 ; −1 ; i ; −i ; 1
2+ i√3 2; 1 + i ; (1 −i)8.
II.2 FORMULES de MOIVRE et D’EULER
Théorème 3 Formules de MOIVRE : Pour tout θet tout entier n:
•(cosθ + isinθ)n=cos(nθ) + isin(nθ) (reformulation de (eiθ)n=einθ )
•(cosθ −isinθ)n=cos(nθ)−isin(nθ) (changement en −θdans la formule précédente)
Formules d’EULER :
Pour tout réel θ:cosθ =eiθ+e−iθ
2et sinθ =eiθ−e−iθ 2i
III Nombres complexes en géométrie
III.1 Module et argument de l’affixe d’un vecteur
Soit ~w un vecteur d’affixe z~w et Ale point tel que −→ OA =~w.
D’après ce qui précède, z~w =z−−→
OA =zA−zO=zAcar zO= 0,
donc nous avons :
|z~w |=|zA|=OA =||~w||
arg(z~w ) = arg(zA) = (~u, −→ OA) = (~u, ~w)[2π]
0~u
~v
A
r=OA
θ
~w
My Maths Space 3 sur 5

TS Chapitre 10 : Les nombres complexes (2ème partie) 2012-2013
III.1.1 Module et argument de zB−zA
Théorème 4 Aet Bsont deux points d’affixes respectives zAet zBdans le plan complexe repéré par (O;~u, ~v)
orthonormé. On a :
|zB−zA|=AB
démonstration : ......
Exemple 3 Soit A(1 −2i),B(3 + 2i)et C(−3). Quelle est la nature du triangle ABC ?
=⇒Utilisation dans la recherche d’ensemble de points :
•M(z) vérifie |z−z1|=r(r > 0). On pose ......
•M(z) vérifie |z−z1|=|z−z2|. On pose ......
Exemple 4 Quel est l’ensemble des points M(z)qui vérifient |z+ 3i|=|z−1 + i|?
Théorème 5 Aet Bsont deux points d’affixes respectives zAet zBdans le plan complexe repéré par (O;~u, ~v)
orthonormé direct. On a :
arg(zB−zA) = (−→ u;−−→ AB)
démonstration : ......
Exemple 5 Soit A(−2−2i),B(3 + 3i). Calculer (−→ u;−→ BA).
Remarque 1 Il faudra être vigilant car |zB−zA|=|zA−zB|en effet AB =BA mais arg(zB−zA)6=arg(zA−zB).
A vérifier .......
My Maths Space 4 sur 5

TS Chapitre 10 : Les nombres complexes (2ème partie) 2012-2013
III.1.2 Module et argument de zD−zC
zB−zA
Propriété 1 Soit ~w et ~ w′des vecteurs non nuls d’affixes respectives z~w et z~
w′, on a :
arg z˜
w′
z˜w = (˜w,˜
w′) (2π)
démonstration : ......
Propriétés :
Soit ˜w et ˜ w′des vecteurs non nuls d’affixes respectives z~w et z~
w′.
•˜w et ˜ w′colinéaires ⇔z˜
w′
z˜w
réel ;
•˜w et ˜ w′orthogonaux ⇔z˜
w′
z˜w
imaginaire pur .
Exemple 6 d’utilisation :
A, B, C et Dsont quatre points deux à deux distincts d’affixes respectives zA, zB, zcet zD. Exprimer en fonction d’un angle orienté
de vecteurs argzD−zC
zB−zA. Exprimer 
zD−zC
zB−zA
en fonction de AB et CD.
Propriété 2 En résumé,
zD−zC
zB−zA
=CD
AB et argzD−zC zB−zA= (−−→
AB;−−→ CD) (2π)
Remarque 2 En particulier, 
zC−zA
zB−zA
=......
...... et argzC−zA zB−zA=...................... (2π)
EXERCICE 4 Reprendre l’exemple 3 et prouver, en utilisant la relation avec les angles orientés de vecteurs que le
triangle ABC est rectangle en A.
My Maths Space 5 sur 5