TP 1 corrige

TP1: Statistique
application chapitre 2

Question 1
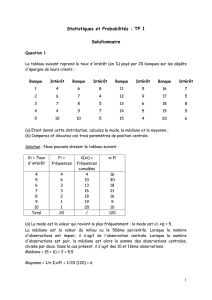
Le tableau suivant reprend le taux d'intérêt (en %) payé
par 20 banques sur les dépôts d'épargne de leurs clients :
(a) Etant donné cette distribution, calculez le mode, la
médiane et la moyenne ;
(b) Comparez et discutez ces trois paramètres de position
centrale. avec fifréquence absolue
Banque Intérêt Banque Intérêt Banque Intérêt Banque Intérêt
1 4 6 8 11 516 7
2 6 7 4 12 917 5
3 7 8 5 13 618 8
4 4 9 7 14 519 5
510 10 515 420 6

Question 1
Mode, médiane et moyenne: paramètres de centre
Le mode est la valeur qui revient le plus
fréquemment.
La médiane est la valeur du milieu ou le 50ème
percentile. Nombre d'observations impair =>
observation centrale Nombre d'observations pair
=> la somme des observations centrales, divisée
par deux.
Moyenne
Attention type de variables
NX...........XX
XMoyenne N21 
Moyenne = 1/N ΣxiFi avec Fi fréquence absolue

Question 1
Sur base des observations, nous construisons un
tableau de fréquences :
avec fifréquence absolue
Xi = Taux
d'intérêt Fi = fréquences C(xi) = fréquences
cumulées
xi Fi
4 4 4 16
5 6 10 30
6 3 13 18
7 3 16 21
8 2 18 16
9 1 19 9
10 120 10
Total 20 /120

Question 1
(a) Le mode est la valeur qui revient le plus
fréquemment : le mode est ici x0 = 5.
Nombre d'observations pair,
observations centrales = 10 et 11ème observations.
Médiane = (5 + 6) / 2 = 5.5
Moyenne = 1/n ΣxiFi = 1/20 (120) = 6
(b) Nous observons dans le cas présent que le mode
et la médiane sont différents de la moyenne avec
x0 < médiane < moyenne. Nous en déduisons par
conséquent que la distribution des taux d'intérêt
parmi les 20 banques belges est asymétrique, ici
étalée vers la droite.