Document

1
SOURCE :Gérard COQUET –LP Guynemer - Grenoble
Baccalauréat Professionnel Vente –Commerce
E.Caudron

2
B
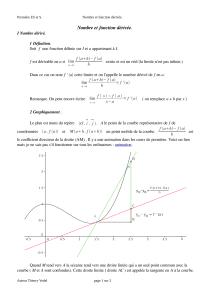
Considérons la fonction f définie par f(x) = x² - 2 sur [-4,5 ; 4,5]
-4,5 -4 -3,5 -3 -2,5 -2 -1,5 -1 - 0,5 0 0,5 1 1,5 2 2,5 3 3,5 4 4,5
-4
-2
0
2
4
6
8
10
12
14
16
18
20
AC
x
xx
X-4 -3 -2 -1 0 1 2 3 4
F(x) 14 7 2 -1 -1-2 2 7 14

3
B
Considérons la fonction f définie par f(x) = x² - 2 sur [-4,5 ; 4,5]
-4,5 -4 -3,5 -3 -2,5 -2 -1,5 -1 - 0,5 0 0,5 1 1,5 2 2,5 3 3,5 4 4,5
-4
-2
0
2
4
6
8
10
12
14
16
18
20
A
Points de la courbe A B C
Abscisse des points
Pente de la tangente
C
3
6
0
0
-3
-6 x2
x
xx

4
Conclusion: • Le tableau de valeurs obtenu est celui d’une
fonction linéaire g définie par g(x) = 2.x
•Cette nouvelle fonction est appelée fonction dérivée de la
fonction f ;Elle est notée f ’
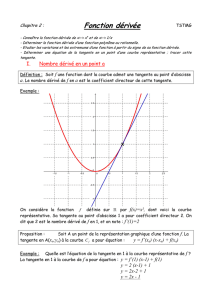
•La pente de la tangente en un point de la courbe, d’abscisse
donnée, est appelée nombre dérivé de la fonction f
f(x) = x²- 2 f’(x) = 2.x
Exemple: Pour x = 3 on a: f’(3) = 2 x3 = 6

5
Dérivées des fonctions usuelles
Fonctions Fonctions dérivées
f(x)= a.x + b a . x + bf’(x) =
f(x) = x² 2f’(x)= x ²
f(x) = x3x 2 3f’(x)=
f(x) = x
1f’(x)= x2
-1