La trigonométrie regroupe diverses notions liées à la

A
B
C
A
B
C
hypoténuse
Opposé à ABC
adjacent
à ABC
Cos (ABC) =
adjacent
hypoténuse
AB
BC
=
Sin (ABC) =
opposé
hypoténuse
AC
BC
=
Tan (ABC) =
opposé
adjacent
AC
AB
=
AB
BC
ABC = cos-1
(
)
)
ABC = cos-1
(
1
2
ABC = 60°
Fiche de synthèse : LA TRIGONOMÉTRIE
La trigonométrie regroupe diverses notions liées à la mesure et au calcul
des angles et des longueurs des côtés d’un triangle. Elle permet de
calculer des angles à partir de longueurs, et de calculer des longueurs à
partir d’angles.
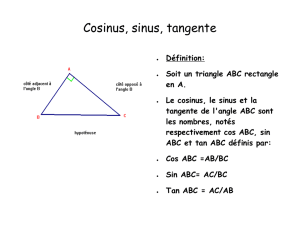
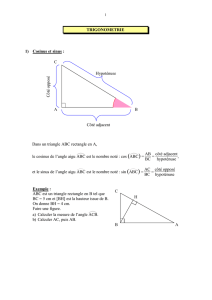
Soit un triangle ABC, rectangle en A.
Différentes fonctions trigonométriques vont permettre de calculer les
longueurs et les angles de ce triangle :
- Le cosinus :
- Le sinus :
- La tangente :
Dans un premier temps, intéressons-nous au cosinus. Il permet de
calculer la mesure d’un angle. Pour cela, il faut connaître les longueurs du
côté adjacent et de l’hypoténuse.
Pour calculer la mesure d’un angle avec le cosinus, on utilise l’inverse du
cosinus.
Par exemple, on cherche à calculer ABC avec AB = 1 et BC = 2.
Sur la calculatrice, il faut utiliser la touche cos-1 ou bien la touche Arccos.

AC
ABC = sin-1
A
B
C
A
B
C
A
B
C
BC
AB
1
Cos ABC
=
BC ×
cos ABC
AB
=
6 ×
cos 60°
=
3
=
AB
(
1
2
ABC = sin-1
)
donc ABC = 30°
(
BC
)
AC
BC
AC
1
=
sin ABC
=
BC ×
sin ABC
sin 30°
=
4 ×
= 2
Le cosinus permet également de calculer la longueur d’un côté d’un
triangle. Pour cela, il est nécessaire de connaître la mesure d’un angle et
la longueur du côté adjacent ou de l’hypoténuse.
Pour calculer la longueur d’un côté avec le cosinus, on utilise le calcul en
croix.
Par exemple, on veut calculer la mesure du côté AB avec BC = 6 et ABC = 60°.
On sait que
Donc
Le calcul d’angle dans un triangle rectangle est également possible avec
la fonction trigonométrique du sinus.
Pour utiliser cette formule, il est nécessaire de connaître la longueur du
côté adjacent et la longueur de l’hypoténuse.
De la même façon que pour le cosinus, on utilise l’inverse du sinus pour
calculer la mesure d’un angle.
Par exemple, on cherche à calculer la mesure de l’angle ABC avec AB = 1
et BC = 2.
Si
alors
Sur la calculatrice, il faut utiliser la touche sin-1 ou bien la touche Arcsin .
A l’inverse, il est également possible de calculer une longueur à partir
du sinus.
Pour cela, il est nécessaire de connaître la mesure d’un angle et la
longueur du côté opposé ou de l’hypoténuse.
Pour calculer la longueur d’un côté, on utilise le calcul en croix.
Par exemple, on sait que BC = 4 et ABC = 30°.
Si
alors

A
B
C
A
B
C
(
AC
AB
ABC = tan-1
)
(
3
3
ABC = tan-1
)
ABC = 45°
AB
AC
1
Tan ABC
=
AC
=
AB×
tan ABC
=
5 ×
tan 45°
= 5
Enfin, on peut utiliser la tangente pour calculer des angles au sein d’un
triangle rectangle. Pour cela, il est nécessaire de connaître les longueurs
du côté adjacent et du côté opposé.
De la même façon que pour le cosinus et le sinus, on utilisera l’inverse de
la tangente pour effectuer ce calcul.
Par exemple, on cherche à calculer la mesure de l’angle ABC avec AC = 3
et AB = 3.
Si
alors
Sur la calculatrice, il faut utiliser la touche tan-1 ou bien la touche Arctan .
A l’inverse, il est possible de calculer une longueur à partir de la
tangente.
Pour cela, il est nécessaire de connaître la mesure d’un angle et la
longueur du côté adjacent ou du coté opposé.
Pour calculer la longueur, on utilise le calcul en croix.
Par exemple, on sait que AB = 5 et ABC = 45°
Si
alors

SinusCosinus
La trigonométrie
> Permet de calculer un angle > Permet de calculer la
longueur d’un côté
A
B
C
> Nécessite :
- Longueurs du
côté adjacent et
de l’hypoténuse
Tangente
> Nécessite :
-Un angle et
- Longueur du
côté adjacent ou
de l’hypoténuse
> Nécessite :
-Longueurs du
côté adjacent et
du côté opposé
> Nécessite :
-Un angle et
- Longueur du
côté adjacent ou
du côtéopposé
> Nécessite :
-Longueurs du
côté opposé et
de l’hypoténuse
> Nécessite :
-Un angle et
- Longueur du
côté opposé ou
de l’hypoténuse
BC
AB
1
Cos ABC =
AB=BC×cos ABC
AB
AC
1
Tan ABC =
AC=AB×tan ABC
BC
AC
1
sin ABC =
AC=BC×sin ABC
A
B
CA
B
CA
B
C
A
B
CA
B
CA
B
C
AB
BC
ABC=cos-1 ()(AC
BC
ABC=sin-1 )(AC
AB
ABC=tan-1 )
Cos(ABC)= Sin (ABC) = Tan (ABC) =
Soit un triangle ABC rectangle en A
hypoténuse
Opposé à ABC
adjacent
à ABC
>Utilisation de
l’inverse
du cosinus
> Exemple :
AB=1etBC=2
)
ABC=cos-1(1
2
ABC=60°
> Utilisation du
calcul en croix
> Exemple :
BC=6et ABC=60°
AB=6×cos 60°=3
>Utilisation de
l’inverse
du sinus
> Exemple :
AC=1etBC=2
(1
2
ABC=sin-1 )
ABC=30°
> Utilisation
du calcul en croix
> Exemple :
BC=4etABC=30°
sin 30°AC=BC×
= 2
>Utilisation de
l’inverse de
la tangente
Exemple :
AC=3etAB=3
(3
3
ABC=tan-1 )
ABC=45°
> Utilisation
du calcul en croix
> Exemple :
AB=5etABC=45
AC=5 ×tan 45°
= 5
adjacent
hypoténuse AB BC
=opposé
hypoténuse AC BC
=opposé
adjacent AC AB
=
SinusCosinus
La trigonométrie
> Permet de calculer un angle > Permet de calculer la
longueur d’un côté
A
B
C
> Nécessite :
- Longueurs du
côté adjacent et
de l’hypoténuse
Tangente
> Nécessite :
-Un angle et
- Longueur du
côté adjacent ou
de l’hypoténuse
> Nécessite :
-Longueurs du
côté adjacent et
du côté opposé
> Nécessite :
-Un angle et
- Longueur du
côté adjacent ou
du côtéopposé
> Nécessite :
-Longueurs du
côté opposé et
de l’hypoténuse
> Nécessite :
-Un angle et
- Longueur du
côté opposé ou
de l’hypoténuse
BC
AB
1
Cos ABC =BC
AB
1
Cos ABC
1
Cos ABC =
AB=BC×cos ABC
AB
AC
1
Tan ABC
1
Tan ABC =
AC=AB×tan ABC AC=AB×tan ABC
BC
AC
1
sin ABC =
AC=BC×sin ABC AC=BC×sin ABC
A
B
CA
B
CA
B
C
A
B
CA
B
CA
B
C
AB
BC
ABC=cos-1 ()
AB
BC
ABC=cos-1 ()(AC
BC
ABC=sin-1 )
(AC
BC
ABC=sin-1 )(AC
AB
ABC=tan-1 )
Cos(ABC)= Sin (ABC) = Tan (ABC) =
Soit un triangle ABC rectangle en A
hypoténuse
Opposé à ABC
adjacent
à ABC
>Utilisation de
l’inverse
du cosinus
> Exemple :
AB=1etBC=2
)
ABC=cos-1(1
2)
ABC=cos-1(1
2
ABC=60°ABC=60°
> Utilisation du
calcul en croix
> Exemple :
BC=6et ABC=60°
AB=6×cos 60°=3AB=6×cos 60°=3
>Utilisation de
l’inverse
du sinus
> Exemple :
AC=1etBC=2
(1
2
ABC=sin-1 )
(1
2
ABC=sin-1 )
ABC=30°ABC=30°
> Utilisation
du calcul en croix
> Exemple :
BC=4etABC=30°
sin 30°AC=BC×
= 2 sin 30°AC=BC× = 2
>Utilisation de
l’inverse de
la tangente
Exemple :
AC=3etAB=3
(3
3
ABC=tan-1 )
ABC=45°ABC=45°
> Utilisation
du calcul en croix
> Exemple :
AB=5etABC=45
AC=5 ×tan 45°
= 5
adjacent
hypoténuse AB BC
=
adjacent
hypoténuse AB BC
=opposé
hypoténuse AC BC
=
opposé
hypoténuse AC BC
=opposé
adjacent AC AB
=
opposé
adjacent AC AB
=