Équations de droites : exercices et méthode graphique

E
EQ QU UA AT TI IO ON NS S D DE E D DR RO OI IT TE ES S
Déterminer l’équation d’une droite par lecture graphique.
Déterminer l’équation d’une droite par lecture graphique.
page 1
Fiche originale réalisée par Thierry Loof
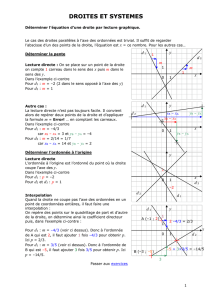
Le cas des droites parallèles à l’axe des ordonnées est trivial. Il suffit de regarder l’abscisse
d’un des points de la droite, l’équation est x = ce nombre. Pour les autres cas…
Déterminer le coefficient directeur
Voir aussi la fiche dédiée
Lecture directe : On se place sur un point de la droite
on compte 1 carreau dans le sens des x puis m dans le
sens des y.
Dans l’exemple ci-contre
Pour d1 : m = –2 (2 dans le sens opposé à l’axe des y)
Pour d2 : m = 1
Autre cas :
La lecture directe n’est pas toujours facile. Il convient
alors de repérer deux points de la droite et d’appliquer
la formule m = yB – yA
xB – xA … en comptant les carreaux.
Dans l’exemple ci-contre
Pour d1 : m = –4/3
car xB – xA = 3 et yB – yA = –4
Pour d2 : m = 2/14 = 1/7
car xB – xA = 14 et yB – yA = 2
Déterminer l’ordonnée à l’origine
Voir aussi la fiche dédiée
Lecture directe
L’ordonnée à l’origine est l’ordonné du point où la droite
coupe l’axe des y.
Dans l’exemple ci-contre
Pour d1 : p = –2
Pour d2 et d3 : p = 1
Interpolation (pour les bons seulement)
Quand la droite ne coupe pas l’axe des ordonnées en un
point de coordonnées entières, il faut faire une
interpolation :
On repère des points sur le quadrillage de part et d’autre
de la droite, on détermine ainsi le coefficient directeur
puis, dans l’exemple ci-contre :
Pour d1 : m = –4/3 (voir ci dessus). Donc à l’ordonnée
de A qui est 2, il faut ajouter 1 fois –4/3 pour obtenir p.
Ici p = 2/3.
Pour d1 : m = 3/5 (voir ci dessus). Donc à l’ordonnée de
B qui est –5, il faut ajouter 3 fois 3/5 pour obtenir p. Ici
p = –14/5.
Passer aux exercices
x
y
1
1
0
d 1
m
d 2
1
1
m
x
y
1
1
0
d 1
xB – xA
d 2
yB – yA
yB – yA
xB – xA
x
y
1
1
0
d 2
–2
d 3
d 1
x
y
1
1
0
d 2
d 1
A (–1 ; 2)
1
B (–3 ; –5)
2 –4/3 = 2/3
–5 + 3×3/5 = –14/5
3

E
EQ QU UA AT TI IO ON NS S D DE E D DR RO OI IT TE ES S
Déterminer l’équation d’une droite par lecture graphique.
Déterminer l’équation d’une droite par lecture graphique.
page 2
Fiche originale réalisée par Thierry Loof
Exercice 1
Par lecture graphique, déterminer l’équation
des droites ci–contre
Corrigé – Revoir les explications du cours
Exercice 2
Par lecture graphique, déterminer l’équation
des droites ci–contre
Corrigé– Revoir les explications du cours
x
y
1
1
0
d1
d3
d2
x
y
1
1
0
d1
d3
d2

E
EQ QU UA AT TI IO ON NS S D DE E D DR RO OI IT TE ES S
Déterminer l’équation d’une droite par lecture graphique.
Déterminer l’équation d’une droite par lecture graphique.
page 3
Fiche originale réalisée par Thierry Loof
Corrigé 1
d1 : y = 1
4 x – 2 = x – 8 4
d2 : x = –3
d3 : y = –2x – 5
Retour aux exercices– Revoir les explications du cours
x
y
1
1
0
d1
d3
d2

E
EQ QU UA AT TI IO ON NS S D DE E D DR RO OI IT TE ES S
Déterminer l’équation d’une droite par lecture graphique.
Déterminer l’équation d’une droite par lecture graphique.
page 4
Fiche originale réalisée par Thierry Loof
Corrigé 2
d1 : y = 1
d3 : y = 2x + 5
d1 : y = – 2
3 x – 1
Retour aux exercices– Revoir les explications du cours
x
y
1
1
0
d1
d3
d2