CHAPITRE 18 : POLYGONES REGULIERS

CHAPITRE 18 : POLYGONES REGULIERS
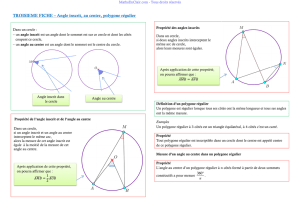
1) DEFINITION.
Un polygone est régulier lorsque ses côtés ont la même longueur et que ses
angles ont la même mesure.
2) PROPRIETE ET DEFINITIONS.
Tout polygone régulier est inscriptible dans un cercle.
Ce cercle est appelé cercle circonscrit au polygone régulier.
Le centre O de ce cercle est appelé le centre du polygone régulier.
3) DERNIERE PROPRIETE.
Soit A et B, deux sommets consécutifs d’un polygone régulier de centre O.
La rotation de centre O et d’angle AOB dans un sens quelconque transforme le
polygone régulier en lui-même.
CONSEQUENCE : Tous les angles au centre, tels AOB, d’un polygone régulier
ont la même mesure.
Exemple
:
Exemple
:
Un triangle équilatéral est
un polygone régulier à trois
côtés.

4) AUTRES EXEMPLES DE POLYGONES REGULIERS.
Carré ABCD Pentagone régulier ABCDE
et son cercle circonscrit et son cercle circonscrit
AOB = BOC = … = 360 : 4 = 90 ° AOB = BOC = … = 360 : 5 = 72 °
Hexagone régulier ABCDEF Octogone régulier
et son cercle circonscrit et son cercle circonscrit
AOB = BOC = … = 360 : 6 = 60 ° AOB = BOC = … = 360 : 8 = 45 °
Exemple
:
La rotation de centre O et d’angle AOB
dans un sens quelconque transforme ce
triangle équilatéral en lui-même.
AOB = BOC = AOC = 360 : 3 = 120 °