La loi normale

Chapitre 8 :
La loi normale
TES
- Connaître la fonction de densité de la loi normale N(0 ;1) et sa représentation graphique.
- Connaître une valeur approchée de la probabilité de l’évènement
[ 1,96;1,96]X 
lorsque X suit la loi
normale N(0 ;1).
- Utiliser une calculatrice ou un tableur pour obtenir une probabilité dans le cadre d’une loi normale
N(μ ;σ²).
- Connaître une valeur approchée de la probabilité des évènements suivants :
[ ; ]X
,
[ 2 ; 2 ]X
et
[ 3 ; 3 ]X
, lorsque X suit la loi normale N(μ ;σ²).
I. Fonction de densité de la loi normale
La loi normale tire son nom du fait qu’elle est bien adaptée pour modéliser des
phénomènes naturels issus de plusieurs évènements aléatoires. On l’appelle aussi loi de
Gauss-Laplace, du nom de 2 grands mathématiciens l’ayant étudiée. Par exemple, la
répartition des tailles d’individus dans une population peut être modélisée par une loi
normale.
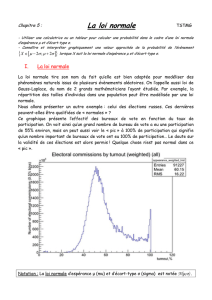
Nous allons présenter un autre exemple : celui des élections russes. Ces dernières
peuvent-elles être qualifiées de « normales » ?
Ce graphique présente l’effectif des bureaux de vote en fonction du taux de
participation. On voit ainsi qu’un grand nombre de bureau de vote a eu une participation
de 55% environ, mais on peut aussi voir le « pic » à 100% de participation qui signifie
qu’un nombre important de bureaux de vote ont eu 100% de participation… Le doute sur
la validité de ces élections est alors permis ! Quelque chose n’est pas normal dans ce
« pic ».

Définition : La loi normale d’espérance μ et d’écart-type σ notée N(μ;σ) est la loi ayant
pour densité de probabilité la fonction f définie sur
par :
2
1
2
1
( ) 2
x
f x e
Exemple : La taille X des hommes en France est modélisée par la loi N(172;14)
Méthode : On choisit au hasard un homme dans la population française.
a) Quelle est la probabilité qu’il mesure entre 1,60m et 1,80m ?
b) Quelle est la probabilité qu’il mesure plus de 2m ?
a) On souhaite calculer P(1,6<X<1,8).
Casio
TI
MENU→STAT→DIST→NORM→Ncd :
Data : Variable
Lower : 160
Upper : 180
σ : 14
μ : 172
(2nd) DISTR→Normalcdf (ou normalFRép) :
normalFRép( 160 , 180 , 172 , 14)
A la calculatrice, on obtient :
P(160<X<180) ≈ 0,5205 à 10-4 près soit 52,05%
b) On souhaite calculer P(200<X).
Casio
TI
MENU→STAT→DIST→NORM→Ncd :
Data : Variable
Lower : 200
Upper : 10^99
σ : 14
μ : 172
(2nd) DISTR→Normalcdf (ou normalFRép) :
normalFRép( 200 , 10^99 , 172 , 14)
A la calculatrice, on obtient :
P(200<X) ≈ 0,0228 à 10-4 près soit 2,28%

Remarques :
- L’espérance est l’abscisse de l’axe de symétrie de la courbe Gaussienne (« en cloche »).
N(-2;1) N(0;1) N(2;1)
- L’écart-type mesure la dispersion des valeurs autour de l’espérance. Plus l’écart-type
est grand et plus les valeurs sont dispersées autour de l’espérance.
N(2;0,5) N(2;1) N(2;2)

II. La loi normale centrée réduite
Propriété : Soit X une variable aléatoire suivant une loi normale N(μ;σ).
La variable aléatoire
X
suit alors une loi normale N(0;1) que l’on appelle loi normale
centrée réduite.
Définition : La loi normale centrée réduite est la loi ayant pour densité de probabilité la
fonction f définie sur
par :
2
2
1
( ) 2
x
f x e
Le tableau de valeurs de la loi normale centrée réduite permet également de calculer
des probabilités de variables suivant une loi normale N(μ;σ).

Propriété : Si X est une variable aléatoire suivant une loi normale N(0;1), alors :
1,96 1,96 0,95P X   
III. Utilisation de la loi normale pour résoudre des problèmes
Propriété : Si X est une variable aléatoire suivant une loi normale d’espérance μ et
d’écart type σ alors :
0,683P X
2 2 0,954P X
3 3 0,997P X
Exemple : En France, la taille des femmes suit une loi normale d’espérance 163cm et
d’écart-type 6cm. On choisit une femme au hasard.
a) Quelle est la probabilité que cette femme mesure entre 157 et 169cm ?
b) Quelle est la probabilité que cette femme mesure entre 151 et 175cm ?
c) Quelle est la probabilité que cette femme mesure entre 145 et 181cm ?
a)
157 169 0,683P X P X
68,3% des femmes mesurent entre 157cm et 169cm
b)
151 175 2 2 0,954P X P X
95,4% des femmes mesurent entre 151cm et 175cm
c)
145 181 3 3 0,997P X P X
99,7% des femmes mesurent entre 145cm et 181cm