cours

INH - ENIHP1 2006-2007 Mathématiques
Calcul d’aire et Calcul intégral : fonctions continues
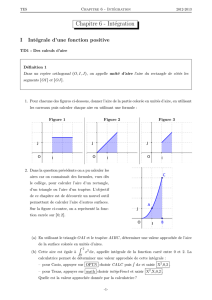
1 Intégrale et calcul d’aire
1.1 Unité d’aire
Définition 1 Soit un repère orthogonal (O, I, J). On appelle unité d’aire, UA, l’aire du rectangle
dont O, I et J forment 3 sommets.
1.2 Calcul d’aire et intégrale
1.2.1 Fonction positive
Définition 2 Soit fune fonction continue positive sur un intervalle [a, b] (a < b). Soit Cfsa courbe
représentative dans un repère orthogonal. L’intégrale de aàbde la fonction f, notée Rb
af(x)dx, est
définie par l’aire exprimée en unité d’aire du domaine Ddélimité par :
– les droites d’équation x=aet x=b,
– l’axe des abscisses et,
– la courbe Cf
On note : Rb
af(x)dx = aire ( D)
Exemple 1 Calculer l’intégrale de -1 à 1 de la fonction f(x) = √1−x2:
0 1−1 0
1
0 1−1 0
1
1.2.2 Fonction négative et de signe quelconque
Définition 3 Soit fune fonction continue négative sur un intervalle [a, b],(a < b). Soit Cf
sa courbe représentative dans un repère orthogonal. L’intégrale de aàbde la fonction f, notée
Rb
af(x)dx, est définie par l’opposé de l’aire exprimée en unité d’aire du domaine Ddélimité par :
– les droites d’équation x=aet x=b,
– l’axe des abscisses et,
– la courbe Cf
On note : Rb
af(x)dx = - aire (D) (aire algébrique)
cours intégration page 1

Exemple 2 Calculer l’intégrale de 0 à 3 de la fonction f(x) = x−4:
0 1 2 3−1 0
1
−1
−2
−3
−4
−5
0 1 2 3−1 0
1
−1
−2
−3
−4
−5
Définition 4 Soit fune fonction continue de signe quelconque sur un intervalle [a, b] (a < b).
Soit Cfsa courbe représentative dans un repère orthogonal. L’intégrale de aàbde la fonction f,
notée Rb
af(x)dx, est définie comme la somme des aires algébriques des domaines définis à partir des
intervalles sur lesquels f(x)garde un signe constant.
On note : Rb
af(x)dx = aire(D1)-aire(D2)+aire(D3)
Remarque 1 La notion d’intégrale se généralise à des fonctions continues par morceaux comme
l’aire algébrique.
Exemple 3 Calculer l’intégrale de 0 à 5 de la fonction en escalier fdéfinie par :
–f(x) = 2 si 0≤x < 2,
–f(x) = −1si 2≤x < 4,
–f(x) = 1 si 4≤x≤5
0 1 2 3 4 5−1 0
1
2
3
4
5
−1
1.3 Valeur moyenne
Définition 5 Soit une fonction fcontinue sur un intervalle [a;b]. On appelle valeur moyenne de
la fonction fsur [a;b]le réel µ=Rb
af(x)dx
b−a.
Remarque 2 Cette définition s’étend à une fonction continue de signe quelconque.
Exemple 4 Calculer la valeur moyenne de f(x) = 1
2x+ 1 sur [0; 5].
0 1 2 3 4 5−1 0
1
2
3
4
5
−1
cours intégration page 2

2 Propriétés d’une intégrale
2.1 Propriétés élémentaires
Proposition 1 Soit fune fonction continue sur un intervalle Iet aet bdeux points de I.
1. Ra
af(x)dx = 0
2. Ra
bf(x)dx =−Rb af(x)dx
3. Relation de Chasles : Rb
af(x)dx =Rc af(x)dx +Rb cf(x)dx avec cun point de I.
4. Linéarité : Rb
a(f+g)(x)dx =Rb af(x)dx +Rb ag(x)dx
et Rb
aλf (x)dx =λ×Rb af(x)dx,λ∈R
2.2 Signe d’un intégrale
Proposition 2 Soit fune fonction continue sur un intervalle [a, b].
– Si f(x)≥0sur [a, b]alors Rb
af(x)dx ≥0(positivité de l’intégrale)
– Si f(x)≤0sur [a, b]alors Rb
af(x)dx ≤0
Démonstration
2.3 Ordre et intégrale
Proposition 3 Soit fet gdeux fonctions continues sur un intervalle [a, b].
Si f(x)≥g(x)sur [a, b]alors Rb
af(x)dx ≥Rb ag(x)dx
Proposition 4 Inégalité de la moyenne
Soit fune fonction continue sur un intervalle [a, b].
Si m≤f(x)≤Msur [a, b]alors m(b−a)≤Rb
af(x)dx ≤M(b−a)
Démonstration
Exemple 5 Justifier sans calculer l’intégrale que π
2√2≤R
π
2
0
dx
√1 + cos x≤π
2
3 Notion de primitive
3.1 Définition
Définition 6 Soit fune fonction définie sur un intervalle I. Une primitive de fsur I, si elle
existe, est une fonction F(x)dérivable sur Itelle que F0(x) = f(x)pour tout xde I.
Remarque 3 La notation usuelle pour écrire une primitive est Rf(x)dx
Exemple 6 Montrer que F(x) = 3x2+ 5x−2est une primitive de f(x) = 6x+ 5 sur R.
cours intégration page 3

3.2 Ensemble des primitives d’une fonction
Proposition 5 Soit fune fonction définie sur un intervalle I. Si Fest une primitive de f, alors :
–fadmet une infinité de primitives sous la forme F(x) + k,k∈R;
– toute primitive de fest de la forme F(x) + k,k∈R.
Démonstration
3.3 Condition d’unicité
Proposition 6 Soit fune fonction définie sur Iet admettant des primitives sur I. Il existe une
unique primitive Gde fsur Ivérifiant la condition G(x0) = y0.
Exemple 7 Trouver la primitive Fde f(x) = 2x−1vérifiant F(2) = 0.
3.4 Primitives usuelles
Primitives et fonctions usuelles :Lecture inverse du tableau des dérivées
f(x) = F(x)sur f(x) = F(x)sur
kcos x
xsin x
xn, n ∈N∗tan x
1
xln x
xα, α ∈R\ {−1}1
1 + x2
ex1
√1−x2
eax
Primitive et opérations sur les fonctions : uétant une fonction dérivable sur I
f(x) = F(x)sur f(x) = F(x)sur
u0(ax +b)u0eu
unu0, n ∈Nu0sin u
uαu0, α ∈R\ {−1}u0
2√u
u0
u
u0
1 + u2
cours intégration page 4