Lesson6et7primitives et intégrales

Leçon 06 et 07 : Primitives et intégrales
Le calcul d’intégrales intervient souvent en fin de problème au BAC.
Définition principale : Soit f une fonction définie et continue sur un intervalle [a ;b],
[ ]
b
a
b
a
)x(Fdt)t(f
∫== F(b) – F(a)
En pratique, ce calcul donne en U.A (unité d’aire), l’aire algébrique (voir croquis ci-dessous)
du domaine du plan (P) compris entre les verticales d’équation x = a et x = b, l’axe des
abscisses y = 0 et la courbe (Cf) d’équation y = f(x).
A comparer le résultat à l’unité d’aire (un carré de 1 sur 1), nous voyons bien qu’en fait l’aire
en dessous de l’axe des abscisses est comptée négativement.
Si on veut avoir l’aire arithmétique alors :
∫ ∫ ∫∫∫
− −− −=−+=
1
1
0
1
1
0
1
0
0
1dt)t(fdt)t(fdt)t(fdt)t(fdt)t(f (à multiplier par 1U.A)
Le bon résultat dans l’exemple est 2.5 U.A.
* Faire une fiche avec les propriétés des intégrales et les primitives des fonctions usuelles.
* Voir le R.O.C démontrant la formule du début.
Important pour le BAC :
L’intégration par parties : Soient u et v deux fonctions intégrables sur [a ;b]
[
[[
[ ]
]]
]
∫
∫∫
∫ ∫
∫∫
∫
−
−−
−=
==
=
b
a
b
a
b
a
dt)t('v)t(u)x(v)x(udt)t(v)t('u
Aire entre deux courbes (Cf) et (Cg), f et g intégrables sur [a ;b] et f(x) ≥ g(x) ∀ x ∈ [a ;b]
Aire arithmétique = A.U1dt)t(g)t(f
b
a
×
××
× −
−−
−
∫
∫∫
∫.
(L’U.A est précisée si
cm1ji == alors 1 U.A = 1 x 1 = 1 cm2)
Passons à la fiche d’exercices.

TERMINALE ES Primitives et Intégrales
Exercice 1
Donner les primitives F
k
des fonctions suivantes :
f(x) = 3x
2
– 5x + 3 ; f(x) = x + 1 +
1
x
3
+
pour x positif ; f(x) = e
−x
; f(x) =
xlnx 1
x ≥ 2 ;
f(x) = 2
x
; f(x) =
3x2
4+ x positifs ; f(x) = (3 – 2x)
2
; f(x) =
2
)1x( 3 − x
≥ 0.
Exercice 2
Calculer les intégrales suivantes :
a) dx
1
x
1x5
3
22
∫
−
−
après avoir décomposé la fonction
1
x
1x5
2
−
−
sous la forme
1
x
b
1
x
a+
+
−.
b)
∫
+
4
0
dx
1x2
1
= c)
∫
π
02dttcos = d)
∫
1
5.0 dxxln =
e)
∫
1
0xdxxe = f)
∫
1
0x2 dxex =
Exercice 3
Dans une architecture moderne, nous trouvons en façade une aire de verre ayant la forme
suivante :
La fonction représentant le haut est f(x) = x
3
4
x
90
2
2
+
−
et la fonction représentant le bas de la structure est :
x
3
2
x
90
1
)x(g
2
+
−
=
a) Montrer que sur l’intervalle [0 ; 60], f(x) ≥ g(x).
b) Calculer l’aire de la surface de verre en m
2
comprise entre les deux courbes.

Exercice 4 Valeur moyenne en économie.
La courbe ci-dessous représente pour chaque instant t, la fonction V donnant le nombre de
produits vendus par un magasin sur 12 mois (V est un polynôme de degré 4) :
Nous savons que V’(0) = V’(6) =V’(12) = 0 et que V(0) = V(12)=1200 et V(6) = 3000.
1) Expliquer pourquoi V’(t) peut s’écrire V’(t) = at(t – 6)(t – 12) a étant un réel que nous
déterminerons par la suite.
2) Comment s’écrit la fonction V(t) ? En utilisant les données sur V(t) déterminer les
constantes apparues dans le calcul, montrer que V(t) peut s’écrire : t∈[0 ; 12]
1200t36t6
4
t
9
50
)t(V
23
4
+
+−=
3) Déterminer la valeur moyenne en utilisant l’intégrale de V entre 0 et 12.
Exercice 5 (Bac)
A. On considère la fonction f définie sur [0 ;+∞[ par f(x) = e
−1.6x + 1.3
1) Etudier cette fonction puis tracer la courbe représentative de f.
2) Soit g tel que g(x) = – xf ’(x). Montrer que G(x) = (−x – 0.625)e
−1.6x+1.3
est une primitive
de g sur [0 ; +∞[.
B. Répartition des revenus
On admet que f étudiée dans la partie A est une bonne modélisation des revenus d’une
population donnée. Le revenu x est donné en centaines de milliers d’€ et la fonction f
donne en milliers d’individus dont le revenu annuel est supérieur ou égal à x.
1) Déterminer le nombre d’individus dont le revenu est supérieur ou égal à 200 000 €.
2) Déterminer le nombre d’individus dont le revenu est compris entre 200 000€ et
250 000 €.
∫
=
q
p
dx)x(g1000R)3
représente la somme des revenus annuels des individus dont le revenu annuel en
centaines de milliers d’€ est compris entre p et q. Déterminer la somme des revenus
annuels des individus dont le revenu annuel est compris entre 2 centaines de milliers d’€
et 2.5 centaines de milliers d’€.
Calculer le revenu annuel moyen d’un individu de ce groupe.

Correction
Exercice 1
Une fonction f définie et continue sur un intervalle [a ; b] possède une infinité de primitives
sur cet intervalle.
f(x) = 3x
2
– 5x + 3 alors F
k
(x) =
.RxetRkkx3
2
x5
x
2
3
∈∈++−
.positifxetRkk)1xln(3x
2
x
)x(Falorspositifxavec
1
x
3
1x)x(f
2
k
∈++++=
+
++=
(Il faut x+1 ≠ 0 et ceci est réalisé avec x positif car x + 1 ≥ 1 > 0 et donc ln (x+1) calculable)
.RxetRkke)x(Falorse)x(f
x
k
x
∈∈+−==
−−
.2xetRkk)x(lnln)x(Falors2xavec
xlnx 1
)x(f
k
≥∈+=≥=
En effet, f est de la forme :
)x(uimplique2xetRkk)x(uln)x(Falors0)x(uavec
)x(u )x('u xln
x
1
)x(f
k
≥∈+=≠==
strictement positif.
.RxetRkk
2ln
2
ke
2ln
1
)x(Falorse2)x(f
x
2lnx
k
2lnxx
∈∈+=+===
f(x) = 3x2
4
+
x positif alors F
k
(x) =
3x24 +
+ k k ∈ R et x positif.
En effet, nous avons une fonction de la forme :
f(x) = 4
)x(u2
)x('u × u(x) strictement positif, les primitives sont de la forme :
F
k
(x) =
)x(u4
+ k , k∈R et u(x) strictement positif.
f(x) = .Rkk
6
)x23(
)x(Falors)x23(
3
k
2
∈+
−
−=−
En effet, nous utilisons la primitive de u
2
(x) soit :
F(x) = 0)x('u
)x('u3 )x(u
3
≠ .
f(x) = .0xetRkk
1x3
)x(Falors0x
)1x( 3
k
2
≥∈+
+
−=≥
+
En effet, nous utilisons une primitive de :
)fautleil'sleajouterfautilet0)x(ufautil,sûrbien(;
)x(u1
)x(Fsoit
)x(u )x('u
)x(f
2
−≠=
−
=
Ces quelques exemples montrent bien qu’il te faut faire une fiche spéciale sur les
primitives et l’apprendre comme tu as appris ta fiche sur les dérivées !

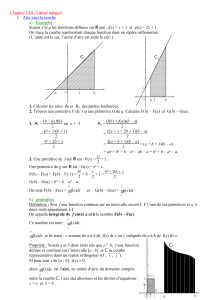
Remarque : nous pouvons représenter quelques éléments d’une famille de primitives.
Par exemple pour : F
k
(x) = − e
−x
+ k x réel.
Représentation de F
k
pour k entier variant de −5 à 5 :
Souvent, il y a une condition supplémentaire par exemple, nous cherchons la primitive telle
que F(0) = 1 alors nous pouvons déterminer k :
F
k
(0) = 1 ⇔ −e
−0
+ k = 1 donne −1+k = 1 soit k = 2. La primitive est alors unique :
F(x) = −e
−x
+ 2 (Voir graphique)
Exercice 2
a) La fonction f(x) =
1
x
1x5
2
−
−
est définie et continue sur l’intervalle [2 ;3], elle est donc
intégrable. Nous devons chercher une primitive de cette fonction pour appliquer la définition
générale mais avant, nous devons la décomposer :
1
x
1x5
2
−
−
=
1
x
b
1
x
a+
+
− ∀x∈[2 ;3], déterminons a et b par identification.
1
x
1x5
2
−
−
=
1
x
)1x(b)1x(a
2
−
−
+
+
1
x
1x5
2
−
−
=
1
x
bax)ba(
2
−
−
+
+
Nous avons donc le système suivant :
a + b = 5 (L1) 2a = 4 donc a = 2
a – b = – 1 (L2) ⇔ 2 – b = – 1 donc
b = 3 .
k=-5
etc...
k=5
2 3 4 5 6 7 8 9 10 11-1-2
2
3
4
5
-1
-2
-3
-4
-5
0 1
1
x
y