1. Définition 2. Image d`un nombre - Antécédent d

1. Définition
Une fonction est un processus de calcul qui permet d'associer à un nombre donné un autre
nombre.
Exemple : Dans l'activité, au nombre 2 représentant la hauteur du triangle on associe l’aire du
triangle : 1
2 × 2 × 2 × 100 – 2² = 2 × 96 = 8 6 ≈ 19,60 cm² à 0,01cm² près
Au nombre 3 on associe 1
2 × 3 × 2 × 100 – 3² = 3 91 ≈ 9,54 cm² à 0,01cm² près
Au nombre 6 on associe 1
2 × 6 × 2 × 100 – 6² = 6 × 64 = 48 cm².
On note A(2) = 8 6 A(3) = 3 91 A(6) = 48.
Au nombre x choisi dans l'intervalle [0 ; 10] représentant la hauteur du triangle, on associe
l’aire du triangle A(x)= 1
2 × x × 2 × 100 – x² = x 100 – x².
A(x) = x 100 – x² est l'expression algébrique de la fonction A.
On dit qu'on a exprimé l’aire A V en fonction de la hauteur du triangle x.
On note A: x
a
x 100 – x²
L'intervalle [0 ; 10] est appelé l'intervalle de définition de la fonction A.
2. Image d'un nombre - Antécédent d'un nombre
On considère la fonction f définie sur l'intervalle [– 3 ; 5] par :
f : x
a
x² – 2 x – 7
f(3) = 32 – 2
×
3 – 7 = – 4
f(5) = 52 – 2
×
5 – 7 = 8
f(– 1) = (– 1)2 – 2
×
(– 1) – 7 = – 4
f(– 2) = (– 2)2 – 2
×
(– 2) – 7 = 1
3 a pour image – 4
5 a pour image 8
l'image de – 2 est 1
l'image de -1 est – 4
– 4 a deux antécédents 3 et – 1
5 est un antécédent de 8
Un nombre de l'intervalle [– 3,5 ; 5] a une seule image.
Un nombre peut avoir 0 ou plusieurs antécédents.

3. Tableau de valeurs
On représente les calculs dans un tableau de valeurs.
x
– 3 – 2 – 1 0 1 2 3 4 5
f(x)
8 1 – 4 – 7 – 8 – 7 – 4 1 8
Ici le pas est 1 car on compte de 1 en 1.
4. Représentation graphique
Les points de la courbe sont les points M du plan dont les coordonnées sont de la forme
M(x ; f(x)).
A(2 ; 4) f(2) = – 7
≠
4 donc A n'est pas sur la courbe.
B(4,5 ; 4,25) f(4,5) = 4,25 donc B est sur la courbe.

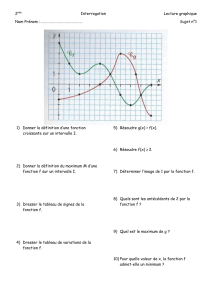
5. Lecture graphique des images et des antécédents
L'image du nombre a est f(a).
Le nombre b a deux antécédents c et d.
6. Maximum, minimum d'une fonction
Définition : Si pour tous les nombres x de l'intervalle I on a :
f(x)
≤
f(a)
alors on dit que f(a) est le maximum de f sur I.
Si pour tous les nombres x de l'intervalle I on a :
f(a)
≤
f(x)
alors on dit que f(a) est le minimum de f sur I.
Exemple:
Pour la fonction f représentée ci-dessus:
5 est le maximum de f sur l'intervalle [– 5 ; 5]. Il est atteint pour x = – 1.
– 5
3 est le minimum de f sur l'intervalle [– 5 ; 5]. Il est atteint pour x = 1