3.1-3.2 Introduction et définition

1
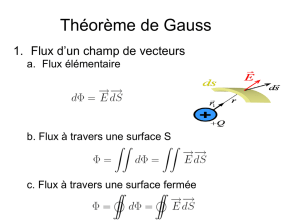
Chapitre 3 Théorème de Gauss
3.0 Introduction
Carl F. Gauss ( 1777-1855 )
Philosophe, mathématicien et physicien
très prolifique
Tiré de www.bibmath.net/bios
Le théorème sert à :
- a) calculer certains champs
électriques par une méthode
géométrique simple.
- c) développer des applications.
- b) fournir des explications
concernant certaines
propriétés de conducteurs
chargés à l’équilibre.
Hyperphysics

2
3.1 Flux électrique ΦΕ
E
cos EdAEdAAdEd ==•=Φ
θ
∫
=Φ EdA
E
R
dA
+
Exemple :Calcul du flux électrique à travers une demi sphère
produit par le champ qui vient de la charge q.
10coscos == θ
Pour un élément de surface
Le flux ΦΕ à travers la demi sphère est donné par 2πkq Nm2/C,
On peut donc calculer un flux à partir d’une charge
∫==Φ dAE
E
CRE
E/Nm 2
22
π =Φ
q
De plus,
2
R
kq
E=
kq
E
π
2=Φ
On obtient
2
2RE
E
π =Φ

3
Calcul du flux : D) Dans un champ non-uniforme E et à travers
une surface de Gauss (fermée)
Exemples de surface de Gauss (fermée)
Surface de Gauss imaginaire
(fermée) Surface mathématique
fermée
2
2
2
r
rhA
π
π
+
=
Cylindre
bclcA 24 +=
l :longueur, b : largeur, c: hauteur
Boîte
2
4rA π
=
Sphère
∫=AAd

4
Calcul du flux : D) Dans un champ non-uniforme E et à travers
une surface de Gauss (fermée)
∫•=Φ AdE
E
Surface de Gauss (fermée)
????=ΦE
Étant donné que le même nombre de lignes
entre et sort, le flux total est défini comme étant
nul.
Convention : Lignes entrant flux négatif et lignes sortant positif
∫
=Φ
θ
cosEdA
E
dA
E
θ cosEdAdE=Φ
0=ΦE
Ici

5
Calcul du flux : E) Dans un champ non-uniforme E et à travers
une surface de Gauss (fermée)
Surface de gauss (fermée)
????=ΦE
Pourquoi y a-t-il plus de lignes qui
sortent ?
Ici le flux est positif
C’est parce qu’il y a des charges positives enfermées à l’
Intérieur.
Combien de charges « q » positives ?
Le théorème de Gauss nous le dira.
∫
= Φ
θ
cos EdA
E
∫ • = Φ A d E
E