Cours 3 - Theoreme de Gauss

Cours 3 – Théorème de Gauss
PHY332
1. Rappel – Introduction
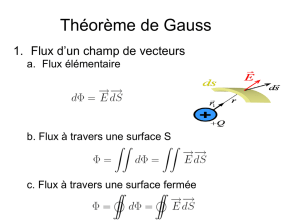
2. Le flux
3. Les symétries
4. Le théorème

À la fin du cours, vous serez capable de déterminer le champ
électrique dans n’importe quelle situation !
2015-08-03
Cours 1 2

Introduction
2015-08-03 Cours 1 3
P
+

Le concept
•Écoulement uniforme d’eau
• est le flux.
▫  
2015-08-03
Cours 1 4
A

Le flux électrique
•Flux électrique :  
2015-08-03
Cours 1 5
 A
Lignes de Champ
A Le flux correspond au nombre
de lignes de champ qui passent
à travers la surface A.
Pour une surface fermée