Module 4209 – Fibres optiques Cours 5 – Interférence Diffraction 1

Module 4209 – Fibres optiques
Cours 5 – Interférence Diffraction
1 . Rappels
1.1 . Onde
Il est courant de voir les ondes écrites sous la forme :
tAtS .sin.
ou sous la forme
S(t)= A.cos (ωt+ϕ)
ou A est l'amplitude, =2.f =2/T est la pulsation (f la fréquence, T sa
période),  une phase.
En notation complexe une onde s'écrit :
S(t)= A.expjωt+ϕ
1.2 . Indice de réfraction
Dans le vide la lumière se propage à la vitesse c. Dans la matière, la lumière se propage à une
vitesse v. On définit l'indice de réfraction
n=c
v
1.3 . Longueur d'onde
La longueur d'onde dans le vide est :
λ= c.T
C'est la longueur parcourue par l'onde pendant
une période T.
Dans la matière la longueur d'onde est
λmat=v.T=c.T
n=λ0 n
1.4 . Phase et déphasage
La phase joue un rôle important en optique.
Le déphasage lié à la propagation d'une onde sur
la distance
Δx
dans un milieu d'indice n est :
ϕ=2πΔx
λmat
=2πnΔx
λ
Les déphasages temporels et spatiaux entre deux
ondes s'expriment : (règle de trois) :
Δ ϕ=2πnΔx
λ
ou
Δ ϕ=2πΔt
T
2 . Interférence
On dit qu'il y a interférence, ou que des ondes interfèrent, lorsque l'intensité résultante de la
superposition de deux ou plusieurs ondes n'est pas la somme de leur intensité. Ce phénomène a
parfois été résumé en optique par l'équation : Lumière + Lumière = Obscurité
2.1 . Démonstration
Considérons une onde
tj
AtS exp.
qui se divise en deux ondes S1 et S2 de même amplitude
et qui se propagent suivant des trajets différents l1 et l2 :

En se propageant de A en B, l'onde S1 accumule un déphasage
ϕ1=2πn L1
λ
et S2
ϕ2=2πn L2
λ
Au moment de se "recombiner" (interférer) en B, les ondes s'écrivent :
1
2.
1
exp
2
nl
tj
A
tS
et l'autre onde est :
2
2.
2
exp
2
nl
tj
A
tS
Après "recombinaison"
Srésultante (t)=S1(t)+S2(t)= A
2expjωt+ϕ1+A 2expjωt+ϕ2 = A 2expjω(t).[exp jϕ1+exp jϕ2]
(Eq. 21)
En posant
2211
21
0
2lnln
et
2211
21
2lnln
on peut écrire :
(Eq. 22 et 23)
01
et
02
.
(Eq. 24 et 25)
En remplaçant 1 et 2 par leurs expressions fonction de 0 et , il vient
00000000
exp.expexp.exp.exp
2
expexp.exp
2
jjjj
tj
jj
tj
B
AA
tS
000
expexp.exp.exp
2
jjj
tj
B
A
tS
soit
0
expcos.
tj
B
AtS
(Eq. 26)
L’onde en B a donc pour amplitude de :
2
2cos.cos.
2211
lnln
AAA
B
(Eq. 27)
 Si la différence de trajets et des indices entre l1 et l2 est telle que  = 0 modulo 2
1cos
, l’amplitude
AA
B
reste inchangée. On parle d'interférence constructive
 Si la différence de trajets et des indices entre l1 et l2 est telle que  =
2
modulo ,
0cos
l’amplitude est nulle
0
B
A
et il n’y a pas de lumière en sortie. On parle
d'interférence destructive
Interférence constructive Interférence destructive

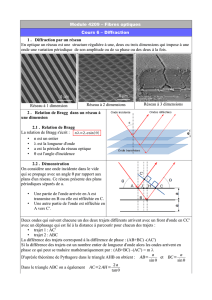
3 . Diffraction par un réseau
En optique un réseau est une structure régulière à une , deux ou trois dimensions qui impose à une
onde une variation périodique de son amplitude ou de sa phase ou des deux à la fois.
4 . Relation de Bragg dans un réseau à
une dimension
4.1 . Relation de Bragg
La relation de Bragg s'écrit :
nλ=2. asin(θ)
•n est un entier
• est la longueur d'onde
•a est la période du réseau optique
• est l'angle d'incidence
4.2 . Démonstration
On considère une onde incidente dans le vide
qui se propage avec un angle  par rapport aux
plans d'un réseau. Ce réseau présente des plans
périodiques séparés de a.
•Une partie de l'onde arrivée en A est
transmise en B ou elle est réfléchie en C.
•Une autre partie de l'onde est réfléchie en
A vers C'.
Deux ondes qui suivent chacune un des deux trajets différents arrivent avec un front d'onde en CC'
avec un déphasage qui est lié à la distance à parcourir pour chacun des trajets :
•trajet 1 : AC'
•trajet 2 : ABC
La différence des trajets correspond à la différence de phase : (AB+BC) -(AC')
Si la différence des trajets est un nombre entier de longueur d'onde alors les ondes arrivent en
phase ce qui peut se traduire mathématiquement par : (AB+BC) -(AC') = m l
D'aprèsle théorème de Pythagore dans le triangle AHB on obtient :
AB=a
sin θ
et
BC=a
sin θ
Dans le triangle ABC on a également
AC=2AH =2a
tan θ
Dans le triangle ACC',
AC '=AC cos(θ)= 2a
tan θcos θ

En remplaçant les différents éléments dans la relation de phase :
mλ= 2a
sin θ− 2a tan θcos θ= 2a sin (θ)[1−cos2(θ)]= 2a sin (θ)sin2(θ)=2asin θ
soit
mλ=2asin θ
5 . Relation de Bragg sous incidence normale
Dans un milieu d'indice n, de période L, pour m=1 et avec un angle d'incidence normal la relation
de Bragg devient :
λ=2nΛ
6 . Réseau photo inscrit dans une fibre
Il est possible d'inscrire un réseau de Bragg de pas L dans une fibre optique. (Fiber Bragg
Grating).
Cela se réalise par photoinscription. Là ou le
cœur de la fibre reçoit une lumière intense
l'indice devient localement n3. On obtient alors
une réflexion pour les ondes de longueur d'onde
λbragg=2nΛ
•Au niveau du réseau photoinscrit la
lumière de longueur d'onde
λBragg
est
réfléchie. (filtre Notch)
•Les autres longueurs d'ondes sont
transmises.
7 . Applications aux filtrages
La première application des FBG est dans les
systèmes de communications pour sélectionner
certaines longueurs d'ondes. (Filtre Notch).
Ils sont aussi utilisés dans les multiplexeurs et
démultiplexeurs optiques avec un circulateur. Ils
rentrent dans la composition des multiplexeurs
optiques d'insertion et d'extraction. (OADM
optical Add Drop Multiplexeur)
OADM : Optical Add Drop Multiplexer
Sur la figure ci contre un OADM avec 4 longueurs d'ondes est représentée. Il est constitué d'un
FBG et de deux circulateurs. Le FBG réfléchie une longueur d'onde (c'est à dire un canal – ici le
canal 4) qui est renvoyée sur le circulateur qui l'extrait (DROP). Puisque le canal a été libérée on
peut y insérer une nouvelle charge par le port DROPP.
Un démultiplexeur optique peut être réalisée en cascadant plusieurs partie extraction d'OADM
pour extraire chacune des longueurs d'onde. Réciproquement un multiplexeur en longueur d'onde
peut être réalisé en cascadant plusieurs fonction INSERTION.