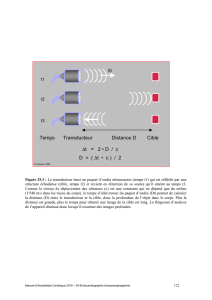
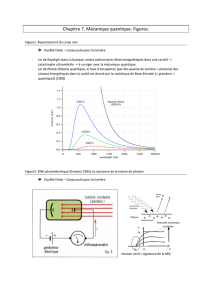
7 - Correction Quantique 17 16 juin 15

Initiation à la mécanique quantique 17
a. L’équation de Schrödinger associée à l’écriture d’une onde stationnaire dans un potentiel V
donne pour solution Ψ(x,t) = A.expi(kx –
E
ℏ
t) avec k
2
=
(
)
0
2
2m E V
−
ℏ
.
En adaptant cette solution, on obtient :
pour la région (I), V = 0, ϕ
1
(x) = A.exp(ik
1
x) + B.exp(– ik
1
x) = A.exp(ik
1
x) + r.A.exp(– ik
1
x)
pour la région (II), V = V
0
, ϕ
2
(x) = C.exp(ik
2
x) = t.A.exp(ik
2
x) (absence de réflexion).
b. Les conditions de raccordement en x = 0, sont ϕ
1
(0) = ϕ
2
(0) et ϕ
1
’(0) = ϕ
2
’(0).
On obtient comme pour les ondes électromagnétiques : 1 + r = t et k
1
(1 – r) = k
2
.t.
r =
1 2
1 2
k k
k k
−
+
< 1 et t =
1
1 2
2k
k k
+
> 1. Si E >> V
0
, k
1
≈ k
2
, t ≈ 1 et r ≈ 0.
On retrouve le cas de la mécanique classique, la particule poursuit son chemin.
c. Aux instants t
1
et t
2
, on observe l’approche du paquet d’ondes incident de la marche de
potentiel. Sa vitesse de déplacement est égale à la vitesse de groupe
1
k
m
ℏ
u
x
.
Á l’instant t
3
, on observe des interférences quantiques entre l’onde incidente et l’onde
réfléchie dans la zone de superposition. La période spatiale des interférences est égale à
une demi-longueur d’onde de De Broglie.
Á l’instant t
4
, le paquet d’ondes incident s’est dissocié en un paquet d’ondes réfléchi et un
paquet d’ondes transmis du côté x > 0. Les amplitudes maximales des ondes réfléchies et
transmises sont déterminées par les probabilités de réflexion et de transmission.
Le schéma montre bien que r < 1 et t > 1.
De l’instant t
4
à l’instant t
5
, on observe le déplacement des différents paquets d’ondes. Le
paquet transmis se déplace à une vitesse inférieure à celle du paquet réfléchi. C’est en
accord avec la diminution de l’énergie cinétique de la particule transmise qui est consécutive
à l’augmentation de l’énergie potentielle.
d. Si E < V
0
,
2
2
k
=
(
)
0
2
2m E V
−
ℏ
< 0. On peut écrire k
2
= iµ, µ > 0, alors ϕ
2
(x) = t.A.exp(– µx).
Par les mêmes relations, on obtient r =
1
1
k i
k i
− µ
+ µ
et |r| = 1 ce qui conduit à R = 1. La particule
quantique est réfléchie par la barrière de potentiel, mais dans la région (II), ϕ
2
(x) est non
nulle pour x <
3
µ
= 3δ alors que la mécanique classique interdit cette région (E
c
< 0).