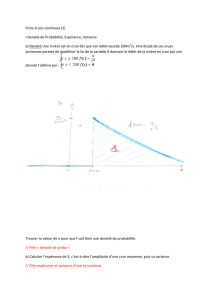
1 Variables aléatoires continues.

f≥0B⊂R
P(X∈B) = ZB f(x)dx
1 = P(X∈R) = Z+∞
∞
f(x)dx
X
X f f(x) = C(4x−2x2) 0 <
x < 2f(x) = 0
CP(X > 0) P(X > 1)
f(x) = λe−x/100
x > 0f(x) = 0
a) 50 150
b) 100
X
F(a) = P(X≤a)
F0(a) = f(a)
P(a≤X≤b) = F(b)−F(a).
F(x)

F
limx→−∞ F(x) = 0
limx→+∞F(x) = 1
a)
X∈ {1,2,3, . . .}
EX=∞
X
k=1
kP(X=k)
f
EX=Z∞
−∞
xf(x)dx
X f g :R→R
Eg(X) = Z∞
−∞
g(x)f(x)dx
X f(x) = 1 0 < x < 1f(x) = 0
EeX

E(aX +b) = aEX+b
E(X+Y) = EX+EY
Var(X) = E(X−EX)2=EX2−(EX)2
Var(aX +b) = a2VarX
X[a, b]
f(x) = 1
b−ax∈[a, b]
0sinon
X∼ U([a, b]

7 15
7 7,30
5 10
L
1/4
E(X) = a+b
2Var(X) = (b−a)2 12
FX(x) = 
0x<a
x−a
b−aa≤x≤b
1x>b
λ > 0X
λ
f(x) = λe−xλ x > 0
0
X∼ E(λ)
EX=1
λVarX=1 λ2
FX(x) = 1−e−xλ x > 0
0
X∼ E(λ)
P(X > t +s|X > t) = P(X > s).
2
a) 2
b) 5
3

n
X X ∼
N(0,1) X
f(x) = 1
√2πe−x2
2,∀x∈R.
Z+∞
−∞
1
√2πe−x2
2dx = 1.
EX= 0 VarX= 1
m∈Rσ2>0X
m σ2fXR
f(x) = 1
σ√2πe−(x−m)2
2σ2.
X∼ N(m, σ2)
EX=m, VarX=σ2
X X ∼
N(0,1)
e−t2
N(0,1))
ΦN(0,1) Φ(a) =
1
√2πRa
−∞ e−t22dt.
ZΦ(a) =
1−Φ(−a).Φ(0) = 1/2
P(|Z| ≤ a) = 2Φ(a)−1.