Sommaire du chapitre 1 - Salim Faci

Chapitre 1 .
4
Sommaire du chapitre 1
1. Le semiconducteur .......................................................................................................... 7
1.1. Structure des bandes d’énergie ................................................................................. 7
1.1.1. Gaps direct et indirect........................................................................................ 7
1.1.2. Les électrons et trous dans un cristal ................................................................ 8
1.1.3. Notion de la masse effective ............................................................................... 8
1.1.3.1. Cas des électrons .......................................................................................... 8
1.1.3.2. Cas des trous ................................................................................................ 9
1.2. Semiconducteur en équilibre .................................................................................. 10
1.2.1. Concentration des porteurs .............................................................................. 10
1.2.1.1. Concentration des porteurs dans les bandes d'énergie ................................ 11
1.2.1.2. Concentration intrinsèque ........................................................................... 12
1.2.2. Position du niveau de Fermi ............................................................................. 12
1.2.3. Semiconducteur extrinsèque ............................................................................ 12
1.2.4. Influence des niveaux d'impuretés – Pièges ...................................................... 13
1.2.4.1. Cas d’un accepteur profond ........................................................................ 13
1.2.4.2. Cas de deux impuretés de type opposé ........................................................ 14
1.3. Semiconducteur hors équilibre ............................................................................... 15
1.3.1. Courant de conduction .................................................................................... 15
1.3.1.1. Vitesse des porteurs .................................................................................... 15
1.3.1.2. Influence de la température sur la mobilité ................................................. 17
1.3.2. Courant de diffusion ........................................................................................ 18
1.3.3. Courant de déplacement .................................................................................. 19
1.4. Paramètres intrinsèques du GaAs ........................................................................... 19
2. Interaction onde radiofréquence – semiconducteur ........................................................ 20
2.1. Equations de Maxwell ............................................................................................. 20
2.2. Ligne de transmission microruban .......................................................................... 21
3. Interaction onde lumineuse – semiconducteur ............................................................... 22
3.1. Effets de l’absorption de photons par un matériau semiconducteur ........................ 22
3.1.1. Condition et coefficient d’absorption ................................................................ 22
3.1.2. Génération de porteurs .................................................................................... 25
3.1.3. Recombinaison directe des porteurs ................................................................. 27
3.1.4. Génération / recombinaison indirecte .............................................................. 28
3.1.5. Recombinaison en surface ............................................................................... 33
3.1.6. Génération / recombinaison Auger .................................................................. 33
3.1.7. Génération par impact ionisant ........................................................................ 34
3.1.8. Dynamique des porteurs dans un semiconducteur éclairé ............................... 35
3.1.8.1. Equations de continuité .............................................................................. 35

Chapitre 1 .
5
3.1.8.2. Diffusion des porteurs ................................................................................. 36
3.1.8.3. Equation de Poisson .................................................................................... 36
3.1.8.4. Retour à l'équilibre ...................................................................................... 37
3.2. Constante diélectrique d'un plasma semiconducteur .............................................. 38
3.2.1. Modèle de Drude – Lorentz ............................................................................... 38
3.2.2. Indice de réfraction .......................................................................................... 39
3.3. Evaluation de la photoconductivité d'un barreau semiconducteur .......................... 40
3.3.1. Domaine de l'infrarouge au visible ................................................................... 40
3.3.2. La photoconductivité ........................................................................................ 40
3.3.2.1. Densité des électrons excédentaires à faible éclairement ............................. 41
3.3.2.2. Densité des électrons libres à fort éclairement ............................................. 43
3.3.2.3. Génération/recombinaison dans GaAs ........................................................ 44
3.3.2.4. Densité de porteurs sous éclairement dépendant du temps ......................... 46
3.4. La photoconductance équivalente ........................................................................... 46
4. Interaction opto-microonde – semiconducteur ............................................................... 46
4.1. Permittivité relative d'un plasma semiconducteur ................................................... 46
4.2. Impédance d'un barreau semiconducteur ............................................................... 48
4.2.1. Formulation du problème ................................................................................ 49
4.2.2. Cas d'un barreau en GaAs ............................................................................... 50
4.2.3. Effet photodiélectrique ..................................................................................... 51
5. Conclusion .................................................................................................................... 52
Références …………………………………………………………………………………………………….53

Chapitre 1 .
6
INTERACTION ONDE ELECTROMAGNETIQUE
SEMICONDUCTEUR
Les mécanismes d’interaction entre une onde électromagnétique et un matériau
semiconducteur diffèrent selon la gamme de la fréquence du rayonnement considéré. Nous
allons discuter ces différents mécanismes dans le cas de l’interaction d'une onde optique
et/ou microonde avec le semiconducteur. Comme nos circuits seront réalisés sur le substrat
d'arséniure de gallium (GaAs), des spécificités et des exemples liés à ce matériau seront
décrits dans ce chapitre.
Ce chapitre débute par un rappel sur les caractéristiques élémentaires des matériaux
semiconducteurs, à savoir leur composition cristalline et les différents mécanismes de
transport de charges.
L’interaction entre un signal microonde et le semiconducteur est ensuite présentée. Nous
nous intéresserons particulièrement à la propagation d'un signal microonde dans une ligne
de transmission en technologie microruban.
Nous poursuivrons par l’interaction de la lumière avec les matériaux semiconducteurs en
développant tous les effets engendrés. Nous définirons la notion d'un plasma
semiconducteur qui représente la base de la commande optique directe des dispositifs
microondes.
Nous terminerons par l’analyse de l’interaction d’une onde électromagnétique avec un
matériau semiconducteur éclairé, c'est-à-dire l'interaction de deux ondes
électromagnétiques de fréquences différentes avec le semiconducteur.

Chapitre 1 .
7
1. Le semiconducteur
Nous allons reprendre quelques notions de base de la physique des semiconducteurs nous
permettant de comprendre les interactions entre une onde électromagnétique et ces milieux.
1.1. Structure des bandes d’énergie
En cristallographie, la description la plus significative des surfaces d’énergie offertes aux
électrons s’effectue dans l’espace des vecteurs d’onde k. Cette description est souvent
simplifiée en considérant les variations de E en fonction de k selon les directions de plus
haute symétrie de cet espace. En se limitant à la première zone de Brillouin, décrite en
annexe A pour l'arséniure de galium, la structure de bandes dans les composés III-V
présente l’allure typique de la figure 1(a). Deux types de structures sont schématisés dans
lequel le niveau 0 eV représente le sommet de la bande de valence. Ce sommet, point Γ, est
situé au centre de la zone de Brillouin (k = 0) et constitué de la convergence de deux bandes.
L'autre structure décrit la bande de conduction pour laquelle plusieurs situations se
présentent suivant la position du minimum. Si ce minimum est situé au même point que 
alors il est unique et le cristal est dit univallée. Si l'emplacement de ce minimum est
différent du point k = 0 et compte tenu de la structure symétrique de la structure cubique
plusieurs minima sont présents. Ces minima sont situés aux points appelés X ou L et le
cristal est dit multivallée. Cette structure est représentée sur la figure 1(b) pour le cas du
silicium.
(a) (b)
Fig. 1. Diagramme de bandes (a) de l'arséniure de gallium et (b) du silicium
1.1.1. Gaps direct et indirect
La largeur énergétique de la bande interdite, aussi appelée gap, représente la différence
entre le minimum absolu de la bande de conduction (niveau Ec) et le maximum absolu de la
bande de valence (niveau Ev).

Chapitre 1 .
8
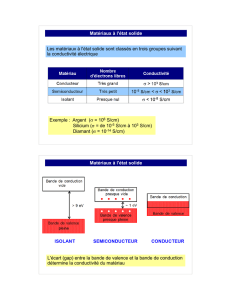
Les structures de bandes des semiconducteurs font apparaître deux types de gaps. Dans le
cas du GaAs, le minimum de la bande de conduction et le maximum de la bande de valence
sont situés pour une même valeur de k (k = 0); les semiconducteurs de ce type sont dits à
gap direct. Dans le cas du silicium, ces extrémums sont situés en deux valeurs de k
différentes et ce type de semiconducteur est dit à gap indirect. La nature du gap joue un
rôle déterminant dans l'interaction du semiconducteur avec un rayonnement
électromagnétique.
1.1.2. Les électrons et trous dans un cristal
Les niveaux de plus basses énergies correspondent à des électrons fortement liés aux
atomes du réseau cristallin et qui s'appellent niveaux du cœur. Par contre, les niveaux de
plus hautes énergies, correspondant aux couches externes, permettent un transfert
relativement facile des électrons dans le matériau. Ces couches constituent les bandes de
valence et conduction.
Dans la bande de valence, les électrons constituent des liaisons chimiques et dans la bande
de conduction ils circulent aisément à travers l'ensemble du réseau. Les électrons les plus
susceptibles de passer de la bande de valence vers la bande de conduction sont les électrons
de la bande supérieure. Ces électrons occupent la bande de conduction inférieure et
donnent naissance à des trous dans la bande de valence. De plus, parmi les états de ces
bandes, ceux qui jouent un rôle essentiel sont ceux du sommet de la bande de valence et du
minimum de la bande de conduction.
1.1.3. Notion de la masse effective
Le déplacement des électrons et trous dans le semiconducteur est différent de leur
déplacement dans le vide en raison des interactions avec les différents atomes du réseau
cristallin. Ces interactions sont différentes suivant les directions du déplacement à
l'intérieur du cristal (périodicité des atomes différente par exemple) et par conséquent le
comportement électrique sera différent.
1.1.3.1. Cas des électrons
Un électron dans un état k dans la bande de conduction est considéré comme une
particule dans un potentiel cristallin. Cette particule quasi-libre de masse m0 est
représentée par une quasi-particule libre de masse me appelée masse effective de l'électron.
L'expression de la masse effective est donnée par (1) qui est reliée à la dérivée seconde de la
courbe des bandes d'énergie E(k) dans l'espace des k (2). Cette masse effective varie donc en
fonction de la courbure des bandes d'énergie.
(1) 
/
(2) 