Corrige_Un consommateur

L2S3 – MASS – Microéconomie – r.foudi –CORRIGE Examen 2014/15– Session 1– Janvier 15 - Page 1 sur 7
BAREME SUR 20 POINTS
4 exercices à 5 points
1 question bonus à 2 points

L2S3 – MASS – Microéconomie – r.foudi –CORRIGE Examen 2014/15– Session 1– Janvier 15 - Page 2 sur 7
Exercice 1 : Consommateur – courbe de prix consommation – (5 points)
Un consommateur dispose d’un revenu R qu’il consacre intégralement à l’achat de deux biens
X et Y, en quantités x et y, au prix respectif px et py.
Sa fonction d’utilité est U = ( x + 10 ) ( y + 6 ) (x et y > 0 et divisibles)
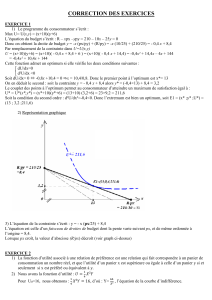
Question 2 : Donner une représentation graphique intuitive du résultat de la question 1.
(NB : cette représentation graphique contient la réponse à la question 3 ci-après)
Question 1
: Déterminer la combinaison optimale des biens (x*,y*) lorsque
R = 210,
px=10
et
py=25. (Méthode
du remplacement)
Le programme du consommateur s’écrit :
Max U= U(x,y) = (x+10)(y+6)
Sc R – xpx –ypy = 210 – 10x – 25y = 0
 y = -x (px/py) + (R/py) = -x (10/25) + (210/25) = - 0,4 x + 8,4
Par remplacement de la contrainte dans U=U(x,y)
U = (x+10)(y+6) = (x+10)( - 0,4 x + 8,4 + 6 ) = (x+10)( - 0,4 x + 14,4) = -0,4x² + 14,4x – 4x + 144
= -0,4x² + 10,4x + 144
Cette fonction admet un optimum si elle vérifie les deux conditions du premier et du second ordre.
Soit 0=
∂
∂
x
U
-0,8x +10,4 = 0
⇒
x = 8,0 4,10 = donc le premier point candidat à l’optimum est x*= 13
On en déduit le second : soit la contrainte y = - 0,4 x + 8,4 alors y* = (-0,4×13) + 8,4 = 3,2
Le couplet de candidats à l’optimum permet au consommateur d’atteindre un maximum de satisfaction égal à :
U* = U*(x*,y*) = (x*+10)(y*+6) = (13+10) (3,2+6) = 23×9,2 = 211,6
Soit la condition du second ordre : 04,00
²
²<−⇔<
∂
∂
x
U L’extremum est bien un optimum, soit
E
1
= (x* ;y* ;U*) = (13 ; 3,2 ;211,6)
0,5
0,5
1

L2S3 – MASS – Microéconomie – r.foudi –CORRIGE Examen 2014/15– Session 1– Janvier 15 - Page 3 sur 7
Question 3 : On considère le prix du bien X comme une variable et égal à px. Donner
l’équation générale de la contrainte budgétaire lorsque R = 210 et py = 25. Donner sa
signification géométrique, et l’illustrer dans le graph lorsque px est décroissant.
Donner sa signification géométrique de cette équation, et l’illustrer par deux droites (en
pointillés) dans le graph lorsque px est croissant.
Question 4 : Ecrire la relation vérifiée par tous les points optimaux, résultant de cette
situation de prix relatif variable et de revenu fixe .
Question 5 : Déduire de cette relation l’équation de la courbe de prix-consommation (CPC)
-dont le résultat est donné ci-dessous-, après avoir rappelé sa définition.
(Rappel pour la démonstration du résultat : une fonction rationnelle, quotient de deux
polynomes, du type : )( )( )( xQ xP xf = peut s’écrire sous la forme
x
b
axf += )( ), a et b étant des
paramètres à déterminer.
L’équation de la contrainte s’écrit : y = - x (
px /25) + 8,4
L’équation est celle d’un faisceau de droites de budget dont la pente varie suivant px, et de même
ordonnée à l’origine = 8,4.
Lorsque px croît, la valeur d’abscisse (R/px) décroît (voir graph ci-dessus)
Cette relation est l’égalité toujours vérifiée à l’optimum :
TMSy/x = px/py avec px variable et py donné
Soit TMS = (y+6)/(x+10) = px/25 (puisque py = 25)
Le résultat à prouver est :
équation de la CPC
Définition de la CPC : Lieu géométrique des optimum correspondant à un effet prix, dans le plan
d’optimisation (y0x).
Détermination de l’équation de la CPC :
1
0,5
0,5
0,5

L2S3 – MASS – Microéconomie – r.foudi –CORRIGE Examen 2014/15– Session 1– Janvier 15 - Page 4 sur 7
Question 6 : Déduire de la CPC, la courbe de demande normale du bien X .
Exercice 2 : Consommateur – courbe d’Engel – (5 points)
La fonction d'utilité d'un consommateur s'écrit :
U(x,y)=2log(x
1
) + 4log(x
2
)
Soient p
1
et p
2
les prix respectifs des biens X
1
et X
2
. R est le revenu du consommateur.
Question : Donner l'équation de la courbe de consommation revenu (CRC), après avoir
rappelé sa définition
Exercice 3 : Elasticités (5 points)
Soit deux biens X et Y, dont la fonction de demande s’écrit respectivement ( avec R, le
revenu, et p les prix) :
1
14
3p R
x= et
2
24p
R
x=
Définition de la C
R
C
:
Lieu géométrique des optimums correspondant à un effet de revenu, dans le plan d’optimisation (y0x).
Détermination de l’équation de la CRC :
La règle : tous les points situés sur la CRC vérifient l’égalité : TMS
2/1
= (U’
x1
/U’
x2
) = rapport des prix = p
1
/p
2
avec U’
x1
= 2/x
1
et U’
x2
= 4/x
2
(en vertu du théorème d(logx)/dx = 1/x)
0,5
1
2
2

L2S3 – MASS – Microéconomie – r.foudi –CORRIGE Examen 2014/15– Session 1– Janvier 15 - Page 5 sur 7
Question 1 : Calculer pour chacun des biens l’élastité prix directe de la demande
Question 2 : Donner la signification du résultat obtenu.
Question 3 : De quelle nature sont les biens x
1
et x
2
?
Exercice 4 : Producteur (5 points)
Soit la fonction de production à deux facteurs
Q = K
0.5
. L
0.25 (K et L >0)
Question 1 : Etudier les rendements d’échelle de cette fonction
Pour les deux biens, lorsque le prix croît de 1%, la demande diminue de 1%
Pour le bien x
1
L’élasticité de la deman
de par rapport au prix étant
≤
-
1, les biens sont dits
«
biens normaux
»
.
Pour le bien x
2
Les rendements dépendent du degrès d’homogénéité (k) de la fonction
Soit : Q(tK
0.5
,tL
0.25
) = t
k
(K
0.5
L
0.25
)
Or
Q(tK
0.5
,tL
0.25
)= tK
0.5
tL
0.25
= t
0.5
K
0.5
.t
0.25
L
0.25
=t
0.5
t
0.25
K
0.5
L
0.25
= t
0.5+0.25
K
0.5
L
0.25
= t
0.75
K
0.5
L
0.25
Par conséquent le degrés d’homogénéité k=0,75<1 . Les rendements sont décroissants . La
croissance des quantités de facteurs entraîne une croissance moins que proportionnelle de la
production.
2 2
0,5
0,5
2