CORRECTION DES EXERCICES

CORRECTION DES EXERCICES
EXERCICE 1
1) Le programme du consommateur s’écrit :
Max U= U(x,y) = (x+10)(y+6)
L’équation du budget s’écrit : R – xpx –ypy = 210 – 10x – 25y = 0
Donc on obtient la droite de budget y = -x (px/py) + (R/py) = -x (10/25) + (210/25) = - 0,4 x + 8,4
Par remplacement de la contrainte dans U=U(x,y)
U = (x+10)(y+6) = (x+10)( - 0,4 x + 8,4 + 6 ) = (x+10)( - 0,4 x + 14,4) = -0,4x² + 14,4x – 4x + 144
= -0,4x² + 10,4x + 144
Cette fonction admet un optimum si elle vérifie les deux conditions suivantes :
dU/dx=0
d²U/dx <0
Soit dU/dx= 0  -0,8x +10,4 = 0 x = 10,4/0,8. Donc le premier point à l’optimum est x*= 13
On en déduit le second : soit la contrainte y = - 0,4 x + 8,4 alors y* = (-0,4×13) + 8,4 = 3,2
Le couplet des points à l’optimum permet au consommateur d’atteindre un maximum de satisfaction égal à :
U* = U*(x*,y*) = (x*+10)(y*+6) = (13+10) (3,2+6) = 23×9,2 = 211,6
Soit la condition du second ordre : d²U/dx²=-0,4<0. Donc l’extremum est bien un optimum, soit E1 = (x* ;y* ;U*) =
(13 ; 3,2 ;211,6)
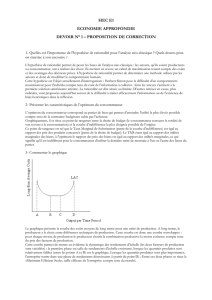
2) Représentation graphique
3) L’équation de la contrainte s’écrit : y = - x (px/25) + 8,4
L’équation est celle d’un faisceau de droites de budget dont la pente varie suivant px, et de même ordonnée à
l’origine = 8,4.
Lorsque px croît, la valeur d’abscisse (R/px) décroît (voir graph ci-dessus)
EXERCICE 2
1) La fonction d’utilité associé à une relation de préférence est une relation qui fait correspondre à un panier de
consommation un nombre réel, et que l’utilité d’un panier x est supérieure ou égale à celle d’un panier y si et
seulement si x est préféré ou équivalent à y.
2) Nous avons la fonction d’utilité :   
Pour U0=16, nous obtenons : 
  , d’où : Y=   , l’équation de la courbe d’indifférence.

Pour tracer la courbe d’indifférence, nous donnons des valeurs à X et en fonction de ces valeurs nous
déterminons Y. Pour X=1, Y=64 ; pour X=2, Y=16 ; pour X=4, Y=4. Le graphique a la forme suivante :
3) L’équation de la droite de budget a la forme suivante : R=XPx+YPy
En remplaçant R=60 et Px=6 et Py=3, nous obtenons 60=6X+3Y Y=20-2X
Pour sa représentation graphique :
- Pour X=1Y=18
- Pour X=2Y=16
- Pour X=3Y=14
Les points où la droite de budget coupe les axes :
- L’axe ox : 
- L’axe oy : 
4) Le taux marginal de substitution du bien Y au bien X en un point quelconque :
TMSY/X
=
 =
5) Le programme de maximisation du consommateur
Max   
6X+3Y=60
Nous savons que : 
 , donc 
 =
 =   =2  X=Y
En remplaçant X par Y, nous avons 6X+3Y=9Y=60  Y=X=20/3