longueur du côté adjacent à cet angle longueur de l`hypoténuse

Trigonométrie
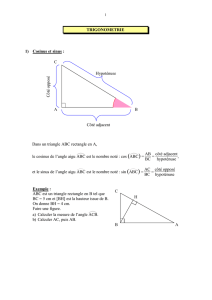
I. Cosinus, sinus et tangente d'un angle aigu dans un triangle rectangle.
1. Définitions
Définitions : Dans un triangle rectangle,
➔le cosinus d'un angle aigu est égal au quotient :
➔le sinus d'un angle aigu est égal au quotient :
➔la tangente d'un angle aigu est égale au quotient :
Exemples :
Dans le triangle ABC rectangle en A,
ex 1, 2, 4, 7 p 183
longueur du côté adjacent à cet angle
longueur de l'hypoténuse
longueur du côté opposé à cet angle
longueur de l'hypoténuse
longueur du côté opposé à cet angle
longueur du côté adjacent à cet angle
sin ABC=longueur du côté opposé à l'angle
ABC
longueur de l'hypoténuse =AC BC
tan ABC=longueur du côté opposé à l'angle
ABC
longueur du côté adjacent à l'angle ABC=AC AB
cos ABC=longueur du côté adjacent à l'angle
ABC
longueur de l'hypoténuse =AB AC

2. Utilisation de la calculatrice
a) Calculer une longueur : calculer ED
Dans le triangle EAD rectangle en E, on a :
D'où, ED ≈ 5,59 cm.
Ex 13, 14, 16, 19 et 23 p 184
b) Calculer un angle
Dans le triangle CAD rectangle en A :
on appuie sur.....
Ex 24, 26 et 27 p 185, 30 p 186
cos EDA=ED
AD , donc
ED = cos EDA× AD =cos 36×6,91≈5,59
sin ACD=AD
CD , donc sin
ACD=6,91
CE + ED , soit sin
ACD≈0,81
ACD≈54,1°

II.Propriétés
Propriétés :
Soit  un angle aigu, alors on a :
➔
tanÂ=sinÂ
cosÂ
➔
sin ²Âcos²Â=1
Exemple :
Soit  un angle aigu.
Sachant que
cosÂ=5
13
, on peut calculer les valeurs exactes de sin  et tan Â.
En effet,
sin²Âcos²Â=sin²Â 5
13 ²=1
d'où
sin ²Â=1− 5
13²=1−25 169=169−25 169 =144 169
or le sinus d'un angle aigu est un nombre toujours positif, donc
sin Â=
144
169=12 13
Puisque
tanÂ=sinÂ
cosÂ
, on a :
tanÂ=12
13÷5 13=12 13×13 5=12 5
Ex 31, 33 et 36 p 186, 38 et 40 p 187, 58 p 190