Cours L3 Chimistes semiconducteurs en cours 2012

Département de physique
Cours « Interface physique-chimie »
Dispositifs électroniques
(éléments de physique des isolants, des semi-conducteurs et quelques exemples de structures de composants)
Rédaction du document : JB Desmoulins (PRAG au Dpt de Physique de l'ENS de Cachan)
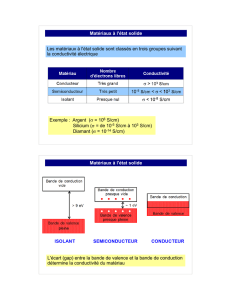
I. Isolant, conducteur, semi-conducteur .
I.1. Niveaux d'énergie d'un atome isolé et d'un atome dans un cristal : bandes d'énergie.
Les niveaux d'énergie d'un atome isolé sont quantifiés. Au zéro absolu, les électrons restent dans les niveaux
d'énergie les plus faibles qui leurs sont permis. Pour des températures plus élevées, les électrons occupant les
niveaux d'énergie les plus élevés (ceux qui les lient le moins à l'atome) peuvent passer dans les niveaux d'énergie
encore plus élevés.
Dans un cristal, chaque atome est soumis à l'influence de ses voisins. En raison des couplages entre atomes,
les niveaux d'énergie vont se subdiviser. Le nombre de niveaux d'énergie permis va alors augmenter.
Dans un cristal, les couplages sont suffisamment forts pour que les états possibles obtenus par subdivision
soient très proches les uns des autres. L'ensemble des états qui résultent d'une subdivision peut alors être assimilé
à une bande continue. Pour la distance interatomique dans un cristal donné (par exemple pour du silicium), on a
alors des bandes d'énergies que les électrons peuvent occuper séparées par une bande qui leurs est interdite.
I.2. Distinction entre matériaux isolants et matériaux conducteurs.
I.2.1. Cas d'un solide au zéro absolu (T=0 K).
Au zéro absolu, tous les niveaux d'énergie les plus bas sont occupés. Seules les bandes d'énergie supérieures
peuvent être partiellement remplies.
Pour qu'il y ait conduction, il faut que l'énergie moyenne des électrons puisse varier. Ceci n'est possible que
dans le cas d'une bande partiellement remplie. On distinguera donc le cas des matériaux dont la bande de
conduction supérieure est totalement remplie qui seront dits isolants, des matériaux dont la bande supérieure est
partiellement remplie qui seront appelés conducteurs.
1

1.2.2. Influence de la température.
Pour une température plus élevée, l'énergie apportée par l'agitation thermique peut permettre à certains
électrons de sauter dans la bande permise supérieure, la rendant ainsi partiellement remplie et donc susceptible
de contribuer à la conduction électrique. Ce passage sera d'autant plus facile que la largeur de la bande interdite
sera plus faible. La largeur de cette bande d'énergie est appelée gap et est noté E
g
.
Par exemple, cette barrière est de 1.1 eV pour le Si et de 0.75 eV pour le Ge. A température ambiante, il est
possible que certains atomes de ces matériaux participent à la conduction. Ils sont alors appelés semi-
conducteurs.
En revanche, pour d'autres matériaux, la bande interdite est trop large et ils seront considérés comme isolants
à température ambiante. C'est par exemple le cas du diamant, pour lequel cette barrière est de 6 eV environ.
I.3. Les matériaux semi-conducteurs.
I.3.1. Semi-conducteur intrinsèque.
Le Si possède 4 électrons sur sa couche périphérique externe. Dans le cristal, les atomes de Si vont mettre en
commun ces électrons et se relier à leurs plus proches voisins par l'intermédiaire de 4 liaisons covalentes. Dans
l'espaces, cela donne une structure tétraédrique. Dans le cas ou un atome de Si perd un électron de sa couche
externe (à cause de l'agitation thermique par exemple), cet électron peut alors participer à la conduction et on dit
qu'il y a génération de porteur. Il apparaît alors un trou (carence d'électron), sur la couche externe de l'atome
de Si considéré. Celui-ci est alors ionisé. Inversement, si un ion Si capte un électron et complète sa couche
périphérique externe, cette disparition de porteur est appelée recombinaison.
Une représentation simplifiée en deux dimensions de l'atome de Si au repos et ionisé est donnée sur la figure
suivante :
Néanmoins, à température ambiante, le nombre d'atomes de semi-conducteur pur (intrinsèque) susceptibles
de participer à la conduction électrique par agitation thermique est très faible (un atome sur 10
13
dans le Si par
exemple ce qui représente environ une densité de porteurs de 10
10
cm
-3
, grandeur qui augmente évidemment avec
la température). Ce matériau n'intéresse pas l'électronicien. Pour être utilisé en électronique, le Si va être enrichi
en atomes susceptibles de contribuer à la conduction électrique. On parle alors de dopage.
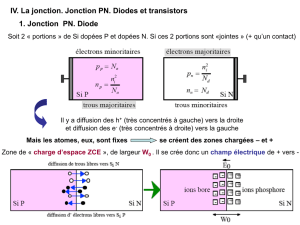
1.3.2. Semi-conducteur dopé.
On ajoute, dans le cristal de semi-conducteur, des impuretés qui ont, soit un électron de valence en plus, soit
un électron de valence en moins. On va les trouver dans la classification périodique :
2

Considérons l'injection d'une impureté qui apporte 5 électrons de valence. Les quatre premiers s'associent
avec les électrons de valence des atomes de Si voisins. En revanche, le cinquième est susceptible de participer à
la conduction. Chaque atome d'impureté apporte donc un électron de conduction. On parle de dopage de type N.
C'est le cas d'une injection d'azote (N), de Phosphore (P), d'Arsenic (As) ou d'Antimoine (Sb).
Dans le cas de l'injection d'atomes qui comportent trois électrons de valence, l'un des atomes de semi-
conducteur voisin ne pourra pas créer de liaison covalente. Chaque atome d'impureté apporte donc un trou. On
parle de dopage de type P. C'est le cas d'une injection de Bore (B), de l'Aluminium (Al), du Gallium (Ga), ou de
l'Indium (In).
Pratiquement, le dopage peut être réalisé par diffusion gazeuse (liée au fait que la concentration d'impuretés
est supérieure dans la gaz), avec par exemple du B
2
H
6
pour un dopage P ou du PH
3
pour un dopage N.
Usuellement, la densité d'atomes dopants reste faible devant celle des atomes de Si. elle est voisine de 10
23
cm
-3
(exemple: 10
15
cm
-3
, 10
18
cm
-3
…). On peut continuer à parler de Si…
1.3.3. Répartition des porteurs dans les bandes de conduction et de valence.
● Densité d'état:
La densité d'état N représente le nombre de places occupables pour un niveau d'énergie E. Cette grandeur,
dépendante de l'énergie électronique E, correspond à la place disponible pour les électrons dans la bande de
conduction N
c
(E) et à la place disponible pour les trous dans la bande de valence N
v
(E). On peu écrire que
N
c
E= 1
2.
2
.2.m
c
h
2
3
/
2
. E−E
c
N
v
E= 1
2.
2
.2.m
v
h
2
3/2
. E
v
−E
Où h=6.626.10
-34
Js est la constante de Planck et m
c
(resp. m
v
) la masse effective de densité d'états dans la
bande de conduction (resp. dans la bande de valence).
● Distribution de Fermi-Dirac:
C'est la probabilité qu'un état occupable soit occupé, c'est à dire le rapport du nombre de places occupées sur
le nombre de places occupables. Elle a la forme suivante :
fE= dn
dN =1
e
E−E
F
k.T
1
3
1.0
0.8
0.6
0.4
0.2
0.0 -0.4 -0.2 0.0 0.2 0.4
E-E
F
(eV)
f(E) pour plusieurs valeurs de T
T=1K ; T=173K
T=273K ; T=373K

La fonction f(E) est appelée distribution de Fermi-Dirac. T est la température absolue, k est la constante de
Boltzman et E
F
est le niveau de Fermi et on s'intéresse aux dn états occupés sur dN états occupables.
Ce niveau représente la référence à l’équilibre thermodynamique. En l’absence de champ extérieur appliqué
et de rayonnement extérieur, ce niveau sera le même dans tous les matériaux dans une structure à l’équilibre.
Nous utiliserons cette remarque importante par la suite pour l’étude des jonctions.
● Nombre de porteurs.
La densité d'électrons n (exprimée généralement en cm
-3
) dans la bande de conduction est alors obtenue en
sommant sur toute la plage d'énergie couverte par cette bande, le produit de la densité d'états par le rapport du
nombre d'états occupés sur le nombre d'états occupables, soit:
n=
∫
E
c
∞
N
c
E.fE.dE
Il faut noter que la fonction que nous venons d'intégrer qui représente la densité de niveau occupés pour chaque
niveau d'énergie, présente un extremum dans la bande de conduction,
De même pour la densité des trous p (exprimée généralement en cm
-3
) dans la bande de valence, la
probabilité d'avoir un trou étant 1-f(E), on a:
p=
∫
−∞
E
v
N
v
E.1−fE.dE
● La figure suivante donne l'allure de f(E), N
c
(E), N
v
(E), f(E).N
c
(E) et (1-f(E)).N
v
(E) quand le niveau de
fermi est au centre de la bande interdite. S'il est plus grand, la densité d'élection va augmenter au détriment de la
densité des trous, S'il est inférieur, ce sera le contraire.
● Pour un semi-conducteur dont le niveau de Fermi E
F
est distant des extrema de plus de 3kT, la fonction de
Fermi se simplifie sous une forme exponentielle et on obtient les densités de porteurs suivantes:
n=N
c
.e
−
E
c
−
E
F
k.T
avec N
c
=
∫
E
c
∞
N
c
E.e
−
E
−
E
c
k.T
.dE
p=N
v
.e
E
v
−
E
F
k.T
avec N
v
=
∫
−∞
E
v
N
v
E.e
E−E
v
k.T
.dE
Où N
c
et N
v
sont les densités équivalentes (ou effectives) d'états. Elles sont une image du nombre d'états
utiles, à la température T, dans les bandes d'énergie.
Conséquences : On remarque que la relation donnée par le produit des densités de porteurs est indépendante
du niveau de Fermi. En effet, on a
n.p=n
i
2
avec n
i
= N
c
.N
v
.e
−
E
c
−
E
v
2.k.T
=gT.e
−
E
g
2.k.T
Où n
i
sera la densité de porteurs intrinsèques (pour le silicium à 300K, n
i
10
10
cm-3). Cette relation est valable
pour les semi-conducteurs intrinsèques mais aussi extrinsèques. Elle ressemble à une loi d'action de masse
comme celle de l'équilibre d'auto-ionisation de l'eau ([H+][OH-]=Ke.
4
cas où E
F
=( E
C
- E
V
)/2
N
v
(E)
N
v
(E).(1-f(E))
N
c
(E)
N
c
(E).f(E)
fonction de Fermi f(E)
E
C
E
V
niveau d'énergie

1.3.4. Commentaires sur la signification du niveau de Fermi E
F
.
● Définition :
Le niveau de Fermi d'un système représente la variation d'énergie libre de ce dernier pour une variation du
nombre de porteurs. C'est le potentiel chimique du système.
● Propriétés:
Pour un système qui n'est pas soumis à une influence extérieure, par exemple un champ électrique extérieur,
ou un flux de photon, le niveau de Fermi doit être constant dans tout le système.
Dans le cas d'un semiconducteur, plus on va doper le système en apportant des électrons pour la conduction
(dope N) plus on va augmenter le niveau de Fermi. Au contraire, plus on va doper le système en apportant des
trous pour la conduction (dopage P), plus on va abaisser le niveau de Fermi.
Si on approche deux éléments indépendants pour en faire un même système, le niveau de Fermi devra être
identique dans les deux sous ensembles du système. L'élément qui a vu son niveau de Fermi augmenter
relativement à l'autre pour que les niveaux s'équilibrent aura reçu des électrons de l'autre élément.
● Cas du semiconducteur intrinsèque:
Dans ce cas, n=p=n
i
. En remplaçant les densités de porteurs par leurs expressions respectives, dans les
égalités précédentes, on peut déterminer le niveau de Fermi pour un semi-conducteur intrinsèque E
Fi
. Sachant
qu'à température ambiante kT est très inférieur au gap, ce niveau se trouve très proche du milieu de la bande
interdite :
E
Fi
=E
c
E
v
2k.T 2.lnN
v
N
c
≃ E
c
E
v
2
Le niveau de Fermi d'un semi-conducteur intrinsèque est donc situé pratiquement au milieu de la bande
interdite. La largeur de cette bande est appelé gap du semi-conducteur qui est noté E
g
.
● Cas du semiconducteur dopé:
Pour le semiconducteur de type N, le niveau de Fermi sera donc plus près de la bande de conduction que de
la bande de valence.
Pour le semiconducteur de type P, le niveau de Fermi sera plus près de la bande de valence que de la bande
de conduction.
● Cas d'un conducteur:
Pour un conducteur, le niveau de Fermi est placé dans la bande de conduction
1.3.5. Evolution de la densité de porteurs de charge.
Dans le semi-conducteur, les phénomènes à prendre en compte pour représenter les mouvements des porteurs
de charge sont la diffusion et l'action d'un champ électrique. La densité de courant de porteurs de charge q
(positive ou négative), dans le cas où le système présente à la fois l'action d'un champ électrique E et un
processus de diffusion s'écrit: 
J
a
=∣q∣.a.µ
a
. E−q.D
a
. grad a
L'évolution de la densité de porteurs de charge dans un volume donné dépendra alors de la densité de
courant, ainsi que des phénomènes de génération (arrivée d'un flux de photon par exemple) et de recombinaison.
Cette évolution est régie par l'équation de continuité
∂a
∂
t
=−1
q
. divJ
a
g
a
−r
a
où a est la densité de porteurs de charge du type considéré, J la densité de courant, g
a
le taux de génération et
r
a
le taux de recombinaison des porteurs considérés (nombre de porteurs générés ou recombinés par unité de
volume et par unité de temps), et q la charge (positive égale à e pour des trous et négative égale à -e pour des
électrons).
Pour établir cette relation en une dimension, il suffit de considérer un volume de section S et de longueur dx.
La variation élémentaire δa.q.S.dx du nombre de charges associées aux porteurs dont la densité volumique est
notée a s'écrit alors
5