document professeur - Académie de Nancy-Metz

Probabilités en terminale
http://images.math.cnrs.fr/Za-normal-noe-raspredelenie.html

2

Taux de participation aux élections
3

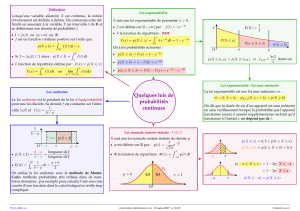
Comment introduire la « loi normale »
Un début d’ exercice « classique »
Une entreprise pharmaceutique fabrique les
comprimés d’un médicament dans deux
machines distinctes A et B. Après une étude
statistique, elle constate que :
- la masse d’un comprimé qui sort de la machine
de fabrication A suit une loi normale de
paramètres µ = 80,00mg et σ = 0,025 ;
- la masse d’un comprimé qui sort de la machine
de fabrication B suit une loi normale de
paramètres µ = 80,00mg et σ = 0,020 ………
4

Du discret au continu
Objectifs :
Introduire la notion de densité de probabilité.
Présenter un exemple d’une variable aléatoire
dont la loi de probabilité est celle d’une loi
normale.
5
Exemple : Les poulets