Rappels

2010
2011
Amelie Caissial – Quentin Grandemange
ESSTIN – 2A S2
2010 2011
Cours de Mécanique du Solide

1
Chapitre 1 : Opérations Vectorielles,
Torseurs – Rappels.
Sommaire
I. Opérations sur les vecteurs – Rappels ............................................................................................ 3
1) Produit scalaire ............................................................................................................................ 3
A) Définition ................................................................................................................................. 3
B) Propriétés ................................................................................................................................ 3
C) Applications ............................................................................................................................. 3
D) Expression analytique .............................................................................................................. 3
2) Produit vectoriel .......................................................................................................................... 3
A) Définition ................................................................................................................................. 3
B) Interprétation géométrique .................................................................................................... 4
C) Propriétés ................................................................................................................................ 4
D) Expression analytique .............................................................................................................. 4
E) Formule du double produit vectoriel (formule de Gibbs) ....................................................... 4
3) Division vectorielle ...................................................................................................................... 4
4) Produit mixte ............................................................................................................................... 5
A) Définition ................................................................................................................................. 5
B) Propriété : Permutation circulaire ........................................................................................... 5
II. Torseur ............................................................................................................................................ 5
1) Définition ..................................................................................................................................... 5
2) Torseur associé à un ensemble de glisseurs................................................................................ 6
A) Ensemble fini de glisseurs ....................................................................................................... 6
B) Ensemble infini de glisseurs .................................................................................................... 6
3) Invariants ..................................................................................................................................... 6
4) Point central – Axe central d’un vecteur ..................................................................................... 6
A) Point central – Définition ........................................................................................................ 6
B) Axe central – Définition ........................................................................................................... 7
C) Recherche de l’axe central ...................................................................................................... 7
5) Opérations sur les torseurs ......................................................................................................... 7
A) Addition ................................................................................................................................... 7
B) Multiplication par un réel  ..................................................................................................... 7

2
6) Torseurs spéciaux ........................................................................................................................ 8
7) Moment d’un torseur – d’un axe ................................................................................................ 8
8) Co-moment (produit) de deux torseurs ...................................................................................... 8
A) Définition ................................................................................................................................. 8
B) Propriétés ................................................................................................................................ 9
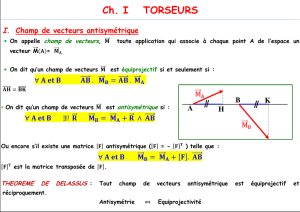
III. Champ équiprojectif .................................................................................................................... 9
1) Définition ..................................................................................................................................... 9
2) Théorème .................................................................................................................................... 9

3
I. Opérations sur les vecteurs – Rappels
1) Produit scalaire
A) Définition
est un réel. 
B) Propriétés
 Symétrie : 
 Distributivité : 
 Multiplicité par un réel :
 Carré scalaire : 
 Cas de nullité :
o 
o 
C) Applications
Si  sont les vecteurs unitaires d’une base orthonormée () :
D) Expression analytique
Dans une base , le produit scalaire des deux vecteurs   et   s’écrit :
2) Produit vectoriel
A) Définition
Le produit vectoriel des deux vecteurs  et  est le vecteur  tel que :
soit  au plan 
 Le repère   soit direct

4
B) Interprétation géométrique
La norme du produit vectoriel 
représente la surface du
parallélogramme ABCD.
C) Propriétés
 Antisymétrie : 
 Distributivité sur l’addition : 
 Multiplication par un réel : 
 Cas de nullité :
o Un des vecteurs est nul
o Les deux vecteurs sont colinéaires
D) Expression analytique
Dans une base orthonormée directe, le produit vectoriel des deux vecteurs   et
 s’écrit :
E) Formule du double produit vectoriel (formule de Gibbs)
3) Division vectorielle
Soit deux vecteurs  et  non nuls déterminant l’ensemble des vecteurs  tel que :  . Le
problème n’est possible que si les deux vecteurs  et  sont orthogonaux.
On considère un plan ( )
A
D
C
B