Chapitre 1 Rappels et Introduction

Chapitre 1
Rappels et Introduction
1.1 Rappels sur les vecteurs.
On se place dans l’espace à trois dimensions, muni d’un repère orthonormé direct
E= (~e1, ~e2, ~e3). Un vecteur ~ Vest repéré par ses trois composantes v1, v2, v3:
~
V=
v1
v2
v3
E
=v1~e1+v2~e2+v3~e3=
3
X
i=1
vi~ei
1.1.1 Somme de deux vecteurs.
Soient deux vecteurs ~ Vet ~ W.
~
V=
v1
v2
v3
E
=
3
X
i=1
vi~eiet ~ W=
w1
w2
w3
E
=
3
X
i=1
wi~ei
Alors,
~
V+~ W=
v1+w1
v2+w2
v3+w3
E
=
3
X
i=1
(vi+wi)~ei.
Exemple :
♦
5

6CHAPITRE 1. RAPPELS ET INTRODUCTION
1.1.2 Multiplication par un scalaire (un nombre).
Soient λun nombre réel et ~ Vun vecteur :
~
V=
v1
v2
v3
E
=
3
X
i=1
vi~ei
Alors, le produit de ~ Vpar λest un vecteur :
λ~ V=
λv1
λv2
λv3
E
=
3
X
i=1
λvi~ei
Exemple :
♦
1.1.3 Produit scalaire de deux vecteurs.
Soient deux vecteurs ~ Vet ~ W.
~
V=
v1
v2
v3
E
=
3
X
i=1
vi~eiet ~ W=
w1
w2
w3
E
=
3
X
i=1
wi~ei
Alors, le produit scalaire de ces deux vecteurs est un nombre réel défini par :
~
V·~ W=v1w1+v2w2+v3w3=
3
X
i=1
viwi
Si ~ Vet ~ Wsont égaux, le produit scalaire est le carré de la longueur du vecteur, le carré
de sa norme
~
V·~ V=
~
V
2
=v2
1+v2 2+v2 3
=longueur de ~ V2
Remarque :
Un vecteur est de longueur nulle si et seulement si v2
1+v2 2+v2 3est nul. Donc si chacune
de ses composantes est nulle. Donc si il est nul. ♦

1.1. RAPPELS SUR LES VECTEURS. 7
Autre définition du produit scalaire :
~
V·~ W=
~
V
~
W
cos ~
V , ~ W
Propriété.
Deux vecteurs sont orthogonaux si et seulement si leur produit scalaire est nul
~
V⊥~ W⇐⇒ ~ V·~ W= 0.
♠
Pour obtenir les composantes d’un vecteur sur une base donnée, on effectue son produit
scalaire avec chacun des vecteurs de la base :
~
V·~ei=vi.
Exemple :
♦
1.1.4 Produit vectoriel de deux vecteurs.
Soient deux vecteurs ~ Vet ~ W.
~
V=
v1
v2
v3
E
=
3
X
i=1
vi~eiet ~ W=
w1
w2
w3
E
=
3
X
i=1
wi~ei
Alors, le produit vectoriel de ces deux vecteurs est un vecteur ~ Udéfini par :
~
U=~ V∧~ W=
v2w3−v3w2
v3w1−v1w3
v1w2−v2w1
ATTENTION !
Le produit vectoriel n’est pas commutatif. ~ V∧~ W=−~ W∧~ V♠

8CHAPITRE 1. RAPPELS ET INTRODUCTION
Le vecteur obtenu est à la fois perpendiculaire à ~ Vet à ~ W. Sa longueur est
~
V
~
W
sin ~
V , ~ W.
C’est l’aire du parallélogramme construit sur ~ Vet sur ~ W. Le trièdre ~ U, ~ V , ~ West direct.
Exemple :
♦
Propriété.
Deux vecteurs sont parallèles si et seulement si leur produit vectoriel est nul.
~
V // ~ W⇐⇒ ~ V∧~ W=~ 0
♠
Formule du double produit vectoriel.
~
U∧~ V∧~ W=~ U·~ W~ V−~ U·~ V~ W♠
1.1.5 Produit mixte de trois vecteurs
Le produit mixte de trois vecteurs ~ U,~ V,~ West un nombre réel
~
U, ~ V , ~ W= det 
u1v1w1
u2v2w2
u3v3w3
=~
U·~ V∧~ W
Ce nombre correspond au volume du parallélépipède construit sur ~ U,~ V,~ W.

1.2. RAPPELS SUR LES TORSEURS. 9
1.2 Rappels sur les torseurs.
Soit ~ Fune force appliquée en un point matériel P. Par définition, le moment en A
de cette force est ~
Mt
Ah~
Fi=−→ AP ∧~ F=~ F∧−→ P A.
On remarque que ~ Mt
Ph~
Fi=~ 0et que ~ Mt
Ah~
Fi·~ F= 0.
Formule du changement de moment.
~
Mt
Bh~
Fi=−−→ BP ∧~ F=−→ BA ∧~ F+−→ AP ∧~ F
| {z }
~
Mt
A[~
F]
♠
1.2.1 Définition.
Dans l’espace à trois dimensions, un torseur [T]est défini par un vecteur libre ~ R
appelé résultante et un champ de vecteurs défini en tout point P, à valeurs ~ Mt
P[T]en
P, tels que :
∀P, ∀Q~ Mt
Q[T] = ~
Mt
P[T] + ~
R∧−→ P Q
~
Mt
P[T]est appelé moment en Pdu torseur [T].~
Ret ~ Mt
P[T]sont les éléments de
réduction du torseur [T], au point P.
Deux torseurs sont égaux, lorsqu’ils ont même résultante et même moment en tout
point. Les définitions imposées impliquent qu’une condition nécessaire et suffi-
sante pour que deux torseurs soient égaux est qu’ils aient mêmes éléments de réduction
en un point.
1.2.2 Propriétés.
√L’ensemble des torseurs forme un espace vectoriel de dimension 6 sur le corps des
réels.
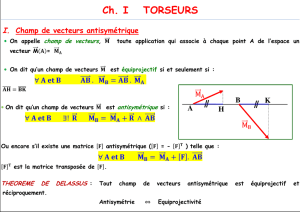
√Le champ des vecteurs P7→ ~
Mt
P[T]est équiprojectif. Autrement dit :
∀P, ∀Q, −→ P Q ·~ Mt
P[T] = −→
P Q ·~ Mt
Q[T].
La projection de ~ Mt
Q[T]sur −→
P Q est égale à la projection de ~ Mt
P[T]sur −→
P Q.
∀P, ∀Q, ~ R·~ Mt
P[T] = ~
R·~ Mt
Q[T].
On note hcette valeur indépendante du point considéré : hest l’invariant scalaire du
torseur [T].