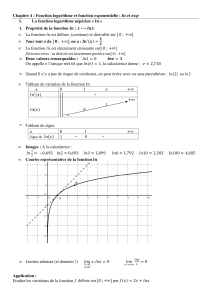
Ebauche d`introduction de la fonction exponentielle

1
Voici une ébauche possible d’une introduction de la fonction exponentielle.
Prérequis : Dérivation - La méthode d’Euler
Activités préparatoires :
1) Un exemple en Physique (la radioactivité)
2) Approximation de la solution par la méthode d’Euler
I. Etude de l’équation f’ = f
On admet l’existence d’une solution
f
de l’équation f’ = f (on pourra la démontrer plus tard).
Première partie : On démontre que la fonction
f
ne s’annule jamais.
On définit la fonction
g
par : Pour tout réel x,
.)()()( xfxfxg 
Cette fonction est dérivable sur R, étant le produit de deux fonctions dérivables sur R.
;0)(';)()()()()(';)(')()()(')('  xgxfxfxfxfxgxfxfxfxfxg
D’où :
.)(;)()()( Kxgxfxfxg 
K
étant une constante. Or :
1)0( f
et
1)0( g
.
Par conséquent, pour tout réel x :
;1)( xg
soit
1)()( xfxf
.
La fonction
f
ne s’annule jamais (On en déduit que : Pour tout réel x,
0)( xf
; f est croissante sur R).
Deuxième partie : On démontre que la fonction
f
est unique.
Supposons que deux fonctions
f
et
g
existent vérifiant :
ff '
et
1)0( f
;
gg '
et
1)0( g
.
Nous savons que chacune de ses fonctions ne s’annule jamais.
Par conséquent, on peut considérer la fonction définie par :
)( )(
)( xg xf x
.
Cette fonction est dérivable sur R, étant le quotient de deux fonctions dérivables sur R.
Pour tout réel x :
;0)(';
)(
)()()()(
)(';
)(
)(')()()('
)(' 22   x
xg
xgxfxgxf
x
xg
xgxfxgxf
x
D’où :
Kx
xg xf
x )(;
)( )(
)(
K
étant une constante. Or :
1)0( f
et
1)0( g
.
Par conséquent, pour tout réel x :
;1)(  x
soit
)()( xgxf 
.
L’équation différentielle
yy '
admet une solution unique notée
exp
, définie sur
R vérifiant
1)0exp( 
.

2
II. Propriétés algébriques de la fonction
exp
.
Pour tous réels a et b :
)exp()exp()exp( baba 
.
Démonstration :
exp
est la fonction solution de l’équation différentielle
yy '
vérifiant
1)0exp( 
.
On veut montrer que : Pour tous réels a et b :
)exp()exp()exp( baba 
.
On définit la fonction
f
par : Pour tous réels x,
)exp( )exp(
)( bbx xf 
, b étant un réel quelconque.(
exp
ne
s’annule jamais).
Cette fonction est dérivable sur R, étant donné que
exp
est dérivable sur R.
Pour tous réels x,
.)()(';
)exp( )exp(
)(';
)exp( )(exp'
)(' xfxf
bbx
xf
bbx
xf 
De plus, on a :
.1)0(;
)exp( )exp(
)0(  f
b
b
f
D’après le résultat du I, on peut affirmer que :
expf
soit pour tous réels x appartenant à R,
)exp( )exp(
)exp( bbx x
, b étant un réel quelconque.
Par conséquent, on peut affirmer que : Pour tous réels a et b :
)exp()exp()exp( baba 
.
On démontre de même que :
Pour tous réels a et b :
)exp( )exp(
)exp( b
a
ba 
.
Pour tous réels a :
)exp(
1
)exp( a a
. (On pose
0a
)
Pour tous réels a et tous entiers relatifs n :
n
ana )exp()exp( 
.
Pour tous entiers relatifs n :
n
n)1exp()exp( 
. (On pose
1a
)
Remarque : Le nombre e, notation ex .
Si l’on pose maintenant exp(1) = e, on obtient : exp(n) = en
(Exercice : recherche d’un encadrement de e…à suivre)
De façon plus générale, en notant exp(x) = ex, pour tous réels x, les propriétés établies ci-dessus s’écrivent
de la façon suivante :
baba eee 
b
a
ba e
e
e
a
ae
e1
La fonction ainsi définie est appelée fonction exponentielle (de base e)
Notation : x
Error!
exp(x) = ex

3
III Etude de la fonction exponentielle
La fonction exponentielle est égale à sa fonction dérivée :
expexp '
.
La fonction exponentielle est strictement croissante sur R.
En effet, la fonction exponentielle est strictement positive.
x
xelim
0lim 
x
xe
On montre que : Pour tout x réel, ex > x.
Démonstration : On définit la fonction
f
par : Pour tous réels x,
xexf x)(
.
Cette fonction est dérivable sur R, étant la différence de deux fonctions dérivables sur R.
Pour tous réels x,
1)('  x exf
.
La fonction
f
est décroissante sur
0;
et croissante sur
;0
. Or :
1)0( f
.
D’où le résultat annoncé. Et :
x
xelim
.
On sait que : Pour tous réels
x
,
x
xe
e1
.
Par conséquent, on a :
0lim 
x
xe
On peut ensuite effectuer le tracé de la courbe.
III. Equation y ’ = ky
Les solutions sur R de l’équation différentielle
kyy'
sont les fonctions
k
f
définie par :
kx
AAexf )(
où A est un réel quelconque.
Démonstration :
Première partie : On démontre que si f est une solution, sur R, de l’équation différentielle
y ’ = ky, alors on a
kx
Aexf )(
avec
A
appartenant à R.
Soit f une solution, sur IR, de l’équation différentielle y ’ = ky
On pose (si k  0) : g(x) = f
x
k. De façon immédiate : g est dérivable sur IR et g’ = g.
On pose alors A = g(0) et h = g
A On a alors h (0) = 1 et h’ = h.
On obtient alors successivement : h : x
Error!
ex puis g : x
Error!
Aex et enfin f : x
Error!
A ekx.
On remarque que si
0k
, on a :
Axf )(
avec
A
appartenant à R.
Deuxième partie : On démontre que si
f
est une fonction définie sur R par
kx
Aexf )(
avec
A
appartenant à R, alors
f
est solution, sur R, de l’équation différentielle y ’ = ky.
On vérifie que toute fonction f : x
Error!
A ekx est telle que f ’ = kf.

4
IV. Relation fonctionnelle caractéristique
Les deux propositions suivantes sont équivalentes :
*
f
est une fonction non nulle dérivable sur R définie par : Pour tous réels a et b :
)()()( bfafbaf 
.
*
f
est une fonction définie sur R par : Pour tous réels x :
kx
exf )(
avec k appartenant à R.
Démonstration :
Première partie :
Si f est la fonction définie par
kx
exf )(
, alors f vérifie la propriété :
Pour tous réels a et b :
)()()( bfafbaf 
.
Deuxième partie : Soit f une fonction, non identiquement nulle, dérivable sur R telle que pour tous réels
a et b :
)()()( bfafbaf 
.
On vérifie alors que
0)0( f
ou
1)0( f
. Si
0)0( f
, alors
0)( af
pour tous réels a , ce qui est
contraire à l’hypothèse.
Donc
1)0( f
.
En dérivant les fonctions :
)( xafx 
et
)()( xfafx 
, on obtient :
Pour tous réels a et b,
)(')()(' bfafbaf 
.
En particulier, pour
0b
, et en posant
f
’(0) = k, on obtient
)()(' akfaf 
(pour tous réels a).
D’après le III, il existe donc un réel A tel que : Pour tous réels a
ka
Aeaf )(
.
Or :
1)0( f
. Donc :
1A
.
Par conséquent, on a : Pour tous réels x
kx
exf )(
.