HEC E1 CONTRÔLE D`ECONOMIE N° 1 – 2011 PROPOSITION DE

HEC E1
CONTRÔLE D’ECONOMIE N° 1 – 2011
PROPOSITION DE CORRECTION
1- Que faut-il entendre par « lois relatives et conditionnelles » dans la réflexion écono-
mique ? (4 points)
Dans le domaine des sciences de la nature, la loi peut se définir comme une relation nécessaire de causali-
té entre deux éléments. La question de la possibilité de déterminer un tel type de lois dans le domaine
économique a été, implicitement ou explicitement, très rapidement posé.
Pour certains économistes, compte tenu des caractéristiques propres des actions économiques, il n’est
possible de construire que des lois « relatives et conditionnelles ». Relatives, c’est à dire qu’elle énoncent
des régularités et non des nécessités absolues (« la plupart des cygnes sont blancs » et non « tous les
cygnes sont blancs »). Conditionnelles, c’est à dire que leur domaine de validité est lié à un contexte géo-
graphique et/ou historique particulier ; dans ce cadre les mutations des économies et de sociétés mènent
à une évolution de la réflexion économique.
2- Christopher Sims, un des deux Prix Nobel d’économie 2011, a déclaré, à propos de
l’usage qu’il entendait faire de la dotation qui accompagne le prix (500 000 euros à peu
près) qu’il allait « la laisser en liquide sur un compte afin d’attendre et réfléchir ». ce
comportement vous paraît-il un exemple de rationalité économique ? (5 points)
N. B. : de nombreuses réponses sont possibles, celle-ci qui suit n’est qu’une proposition
La rationalité économique, entendue dans son sens classique, signifie que l’individu a un objectif simple :
maximiser son utilité compte tenu de ses ressources disponibles en s’appuyant sur une analyse coût-
avantage des décisions possibles.
Dans ce contexte, la décision de Christopher Sims de laisser l’argent en liquide sur un compte (en faisant
l’hypothèse que ce dépôt ne produise pas d’intérêt) apparaît comme peu rationnelle puisque M. Sims re-
noncent à un gain.
Maintenant, l’analyse peut être complexifiée en introduisant la notion de risque, d’une part, et la question
de l’information pertinente d’autre part. Même pour un Prix Nobel d’Économie et, en particulier, dans un
contexte de crise économique et financière, la recherche d’un placement intéressant pour 500 000 euros
peut se révéler complexe et, dans ce cas, il peut être rationnel de supporter un coût lié au travail de col-
lecte d’information et de réflexion. De plus, M. Sims est peut être caractérisé par un niveau d’aversion au
risque relativement élevé, ce qui peut également justifier la mise en œuvre de comportements prudents, la
perte de revenu étant compensée par la certitude de conserver son patrimoine.
3- Qu’est-ce que la valeur utilité ? (2 points)
Le principe de la valeur-utilité signifie que la valeur qu’un individu attribue à un bien dépend de l’utilité
que ce bien lui apporte, cette utilité étant elle-même liée à la plus ou moins grande rareté du bien. Cette
conception, proposée par Condillac et Say et reprise par les économistes néo-classiques, s’oppose à celle
de la valeur travail.
4- Définir une courbe d’indifférence et présenter ses caractéristiques essentielles (4 points)
Une courbe d’indifférence représente l’ensemble des paniers de biens qui procurent la même utilité à un
consommateur. Il est donc indifférent pour le consommateur de choisir un de ces paniers plutôt qu’un
autre.
Les courbes d’indifférences sont décroissantes (pour conserver la même utilité si la quantité d’un bien
dans le panier augmente, celle de l’autre bien doit diminuer), plus elles sont éloignées de l’origine, plus la
satisfaction ressentie par le consommateur est élevée (application de l’hypothèse de non saturation), elles
sont convexes par rapport à l’origine (ce qui signifie que les consommateurs « préfèrent les mélanges ») et
ceux courbes d’indifférence ne peuvent se couper (si elles ont un point en commun alors elles sont néces-
sairement confondues).

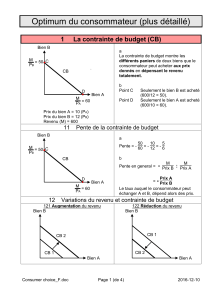
5- Représenter graphiquement l’optimum du consommateur. Vous commenterez le gra-
phique. (5 points)
Représentation graphique : voir le cours
Le commentaire doit faire apparaître les points suivants :
l’optimum du consommateur, qui suppose la maximisation de l’utilité ressentie compte tenu des res-
sources disponibles, doit nécessairement se situer sur la droite de budget (si le panier souhaité se trouve à
gauche de la droite, il reste des ressources inutilisées et on peut atteindre une utilité plus grande ; s’il se
trouve à droite les ressources sont insuffisantes).
On peut alors montrer que l’optimum correspond au point de tangence entre la droite de budget et une
courbe d’indifférence (application des caractéristiques des courbes d’indifférence, il n’existe qu’un point
de tangence possible entre la droite de budget et une courbe d’indifférence sur le plan).
A l’optimum, le rapport des prix des biens composant le panier et de le rapport de leur utilité marginale
sont égaux. Ce qui signifie que l’utilité procurée par la dernière unité de ressource utilisée est indifférente
pour le consommateur quelque soit le bien consommé.
HEC E1
CONTRÔLE D’ECONOMIE
1- Que faut-il entendre par « lois relatives et conditionnelles » dans la réflexion écono-
mique ? (4 points)
2- Christopher Sims, un des deux Prix Nobel d’économie 2011, a déclaré, à propos de
l’usage qu’il entendait faire de la dotation qui accompagne le prix (500 000 euros à peu
près) qu’il allait « la laisser en liquide sur un compte afin d’attendre et réfléchir ». ce
comportement vous paraît-il un exemple de rationalité économique ? (5 points)
3- Qu’est-ce que la valeur utilité ? (2 points)
4- Définir une courbe d’indifférence et présenter ses caractéristiques essentielles (4 points)
5- Représenter graphiquement l’optimum du consommateur. Vous commenterez le gra-
phique. (5 points)