La théorie du consommateur

La théorie du consommateur
On distingue la théorie cardinale et la théorie ordinale
I.
La théorie cardinale de l’utilité
1. La loi de l’utilité marginale décroissante



L’utilité totale est la satisfaction apportée par l’ensemble des unités
consommées. L’utilité marginale est la satisfaction apportée juste par la
dernière unité consommée.
L’utilité qu’un individu retire de la consommation d’unités successives d’un
bien donné diminue au fur et à mesure que la consommation de ce bien
augmente
Pour de nombreux biens, il existe un seuil de satiété au-delà duquel toute
consommation de nouvelles unités du bien ne procure aucune utilité
supplémentaire. La consommation prolongée peut même finir par faire baisser
l’utilité totale, de sorte que la consommation d’unités supplémentaires aurait
une Um négative
2. La loi de l’égalisation des utilités marginales pondérées
Pour étudier l’équilibre du consommateur dans la théorie cardinale, nous allons
distinguer trois situations :
o En situation d’abondance, l’individu cherche à maximiser son utilité totale.
Donc il continuera la consommation du produit jusqu’à ce que l’Um s’annule
o Dans le cadre d’une économie de troc, consommer X c’est renoncer à un
bien Y que l’on aurait pu obtenir en échange. Dans ce cas, l’individu maximise
sa satisfaction en choisissant une combinaison (X,Y) telle que : Umx = Umy
o Dans le cadre d’une économie monétaire, les biens ne s’échangent pas
entre eux mais contre de la monnaie. Le problème du consommateur est donc
de répartir un budget donné entre X et Y. Dans ce cas, il faut égaliser les Um
mais en les pondérant par les prix des biens X et Y (Px et Py). Condition
d’équilibre Umx/Px = Umy/Py
II.
La théorie ordinale de l’utilité
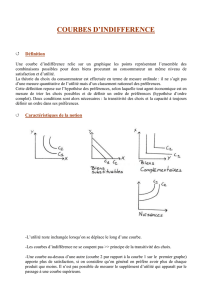
1. Les courbes d’indifférence
o Une courbe d’indifférence représente l’ensemble des combinaisons de deux
biens qui procurent au consommateur un niveau de satisfaction identique
o Les courbes d’indifférence ne peuvent pas se couper
o Les courbes d’indifférence sont décroissantes, ce qui indique que si le
consommateur réduit sa consommation de Y, il doit accroître celle de X pour
conserver un niveau de satisfaction constant.
o Les courbes d’indifférence sont convexes par rapport à l’origine
o Le taux marginal de substitution TMS est défini comme le rapport selon
lequel se fait l’échange entre les deux biens par le consommateur désireux de
maintenir le même niveau de satisfaction. Le TMSxy, mesure la quantité de Y
que le consommateur doit abandonner pour acquérir une plus grande quantité
de X, tout en restant sur la même courbe d’indifférence
TMSxy = - ∆y/∆x
= - dy/dx (lorsque ∆x tend vers 0)
= Umx / Umy
2. Contrainte budgétaire et équilibre du consommateur
o La contrainte budgétaire signifie que la dépense doit être égale au revenu :
R = X Px + Y Py
o On peut représenter graphiquement l’ensemble des combinaisons (X,Y) que
l’individu peut acheter avec un revenu donné par une droite (Y= -Px/Py X +
R/Py) : droite ou ligne budgétaire
o Détermination graphique de l’équilibre du consommateur : la combinaison
optimale est le point où la courbe d’indifférence est tangente à la droite
budgétaire
o Détermination arithmétique de l’équilibre du consommateur : 3 méthodes
o Transformer la fonction de satisfaction en une fonction à une seule
variable puis annuler la dérivée première
o Egaliser les Um pondérés par les prix pour trouver X en fonction de Y
puis remplacer dans la contrainte budgétaire
o La méthode de Lagrange consiste à formuler une nouvelle fonction L à
maximiser en annulant les 3 dérivées partielles
L = U(x,y) + λ (R – XPx – Ypy)