Fiche Méthodologique n°5 Savoir-faire applicables aux données

Fiche Méthodologique n°5
Savoir-faire applicables aux données quantitatives et aux représentations graphiques
L'enseignement des sciences économiques et sociales doit conduire à la maîtrise de savoir-faire quantitatifs, qui ne sont pas exigés
pour eux-mêmes mais pour exploiter des documents statistiques ou pour présenter sous forme graphique une modélisation simple
des comportements économiques ou sociaux.
Calcul, lecture, interprétation
- Proportions, pourcentages de répartition
(y compris leur utilisation pour transformer une table de mobilité en tables de destinée et de recrutement) chapitre n°5
- Propensions moyenne et marginale à consommer et à épargner
- Élasticité comme rapport d'accroissements relatifs
- Mesures de variation : coefficient multiplicateur, taux de variation, indices simples et pondérés
Lecture et interprétation
- Élasticité prix de la demande et de l'offre, élasticité revenu de la demande
- Représentation graphique de fonctions simples (offre et demande) et interprétation de leurs pentes

PROPORTION ET POURCENTAGE DE REPARTITION (Rappels)
Définition
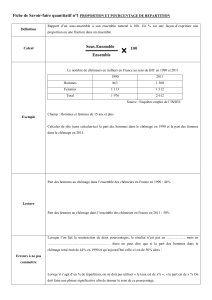
Rapport d’un sous-ensemble à son ensemble ramené à 100. Un % est une façon d’exprimer une
proportion ou une fraction dans un ensemble
Calcul
Exemple
Le nombre de chômeurs en milliers en France au sens du BIT en 1990 et 2011
1990
2011
Hommes
863
1 300
Femmes
1 113
1 312
Total
1 976
2 612
Source : Enquêtes emploi de l’INSEE
Champ : Hommes et femmes de 15 ans et plus
Calculez de tête (sans calculatrice) la part des hommes dans le chômage en 1990 et la part des femmes
dans le chômage en 2011.
Lecture
Part des hommes au chômage dans l’ensemble des chômeurs en France en 1990 : 44%
Part des femmes au chômage dans l’ensemble des chômeurs en France en 2011 : 50%
Erreurs à ne pas
commettre
Lorsque l’on fait la soustraction de deux pourcentages, le résultat n’est pas en ……………. mais en
…………………………………….………. Ainsi on peut dire que si la part des hommes dans le
chômage total était de 44% en 1990 et qu’aujourd’hui celle-ci est de 50% alors :
Lorsqu’il s’agit d’un % de répartition, on ne doit pas utiliser « le taux est de x% », « la part est de x % On
doit faire une phrase significative afin de donner le sens de ce pourcentage.

MESURES DE VARIATION, COEFFICIENT MULTIPLICATEUR, TAUX DE VARIATION
Intérêts
Les variables économiques et sociologiques évoluent dans le temps il s’agit alors de pouvoir mesurer des évolutions.
Les variables économiques et sociologiques peuvent différer d’un groupe social à un autre, d’un pays à un autre etc, il s’agit
alors de pouvoir comparer des grandeurs entre-elles.
Calcul
Calculs pour appréhender une évolution
Variation absolue : Valeur à l’année d’arrivée – Valeur à l’année de départ
Variation relative :
Taux de variation : [(Valeur à l’année d’arrivée – Valeur à l’année de départ) / Valeur de départ] * 100
Coefficient multiplicateur : (Valeur à l’année d’arrivée) / (Valeur à l’année de départ)
On peut donc passer du taux de variation au coefficient multiplicateur et inversement :
Taux de variation = (Coefficient multiplicateur – 1) * 100
Coefficient multiplicateur : (Taux de variation / 100) +1
Calculs pour effectuer une comparaison
Différence absolue : Valeur pour une variable x – Valeur pour une variable y
Différence relative : (Valeur pour x – Valeur pour y ) / Valeur pour y
Coefficient multiplicateur : (Valeur pour une variable x) / (Valeur pour une variable y)
Exemple
De combien a augmenté le nombre de chômeurs hommes en France de 1990 à 2011 ? (Faire de tête les trois calculs possibles)
Comparer le nombre de chômeurs hommes et le nombre de chômeurs femmes en France en 1990 (Faire de tête deux calculs)
Le taux de chômage en France au sens du BIT en 1975 et en 2010 en %
1975
2010
Hommes
2,6
9,0
Femmes
4,7
9,7
Total
3,4
9,4
Source : Enquêtes emploi de l’INSEE
Faites une phrase significative avec le taux de chômage des hommes en France en 2010 (9,0)
De combien a augmenté le taux de chômage en France de 1975 à 2010 (trois calculs attendus).
Lecture
Quels que soient les résultats d’un calcul d’évolution, la phrase de présentation des résultats doit impérativement comporter les éléments
suivants : La date ou la période ; le pays ou la zone géographique concernée ; la variable étudiée ; le sens de l’évolution (augmentation /
diminution). l’unité et la source. Il ne faut pas employer le mot taux de variation dans la phrase.

INDICES SIMPLES ET PONDERES
Définition
L’indice d’une valeur est le rapport de cette valeur à une valeur de référence appelée « base » et à laquelle est affecté par
convention l’indice 100.
Un indice peut permettre de calculer une évolution relative (comme le taux de variation ou le coefficient multiplicateur).
Un indice peut permettre d’effectuer une comparaison (comme le coefficient multiplicateur)
Calcul
Dans le cas d’une évolution pour obtenir un indice il faut :
Prendre une année de référence
Diviser toutes les valeurs de la série par la valeur de cette année de référence (y compris la valeur de l’année de référence)
Multiplier chaque résultat par 100 afin d’avoir un indice base 100 (à l’année de référence)
Dans le cas d’une comparaison pour obtenir un indice il faut faire les mêmes calculs en prenant comme référence un pays,
un groupe social, une classe d’âge etc.
Lecture
Par rapport à l’année de base ou à la variable de base la lecture est extrêmement simple car pour obtenir un coefficient
multiplicateur il suffit de diviser la valeur considérée par 100 ; pour obtenir un taux de variation (en %) dans le temps il suffit
d’enlever 100 à l’indice observé pour obtenir le taux de variation, laquelle se lit à partir de l’année de base.
Exemples
Productivité par tête
1913
1950
1973
2010
Etats-Unis
France
15 700
8 422
30 500
13 684
48 888
38 571
88 068
71 953
A l’aide d’une machine à calculer complétez les deux tableaux :
Productivité par tête
1913
1950
1973
2010
Etats-Unis
France
100
100
Productivité par tête
1913
1950
1973
2010
Etats-Unis
France
100
100
100
100
Erreurs à ne pas commettre

ÉLASTICITE COMME RAPPORT D'ACCROISSEMENTS RELATIFS
Définition
L’élasticité désigne la variation relative d’une grandeur (effet)
par rapport à la variation relative d’une autre grandeur (cause).
Calcul
Exemples et lecture
Lorsque A varie de +3% alors B varie de +2%
Elasticité de B par rapport à A
Lorsque A varie de +3% alors B varie de +5%
Elasticité de B par rapport à A
Lorsque A varie de +3% alors B varie de -2%
Elasticité de B par rapport à A