étude cinématique du mouvement d`un solide

Étude cinématique du mouvement
d’un solide
corrigé
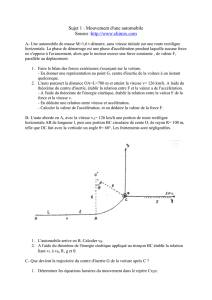
Un mobile M peut glisser sans frottement le long de la
ligne de plus grande pente x'Ox d'un plan incliné
faisant un angle  par rapport au plan horizontal. Il est
attaché à un fil inextensible tendu parallèlement à l'axe
x'Ox . Ce fil exerce une force de traction de norme T
sur le mobile. À l'instant t = 0, le mobile M est au repos
son centre d'inertie est en O (origine de l'axe), et on
applique au fil une traction qui fait gravir à M le plan
incliné ; à l'instant t1 = 2,0 s, le fil casse (Masse du
mobile : m = 1 kg. )
Un capteur optique, couplé à un ordinateur, mesure la
vitesse vx du mobile.. Le graphique vx = f(t) est donné
ci-dessous. On prendra g =10 m.s-2.,  =14,5°.
Dans un premier temps on s'intéressera au
mouvement du mobile entre l'instant t compris entre 0
et 2 secondes .
Q1
a) Définir le système, le référentiel, le repère, la
somme des forces extérieures, bref faire l'étude
mécanique.
b) Enoncer la loi permettant de déterminer les valeurs
des coordonnées a x et a y du vecteur accélération du
centre d'inertie du mobile.
c) Donner l'expression littérale de ces coordonnées en
fonction des coordonnées des vecteurs force et de
l'angle  dans le repère que vous avez choisi.
Q2
a) A l'aide du graphique déterminer la valeur de ax.
b) En déduire l'expression de vx(t).
c) Calculer la valeur de la force de traction T.
d) Quelle est l'influence de la masse sur l'accélération
ax, à force de traction constante ? Pourquoi ?
Q3
a) Donner l'expression de la distance parcourue x, en
fonction de l'accélération ax et du temps.
b) En déduire la distance x parcourue par le mobile
avant que le fil ne casse.
c) De quel type de mouvement s'agit-il ?
On s'intéressera maintenant à la seconde phase :
le fil casse.
Q4
a) Faire l'étude mécanique .
b) Déterminer l'expression puis la valeur de
l'accélération ax en fonction de g et de l'angle .
c) De quel type de mouvement s'agit-il ?
Q5
1) Déterminer graphiquement la valeur de ax.
2) Donner l'expression littérale puis numérique de vx(t),
on prendra comme origine des temps t = 2 s.
3) A partir de quel instant compté, à partir du début du
mouvement, le mobile redescend t-il la pente ?
fil
y
O
x
Mobile M
-1,5
-1
-0,5
0
0,5
1
1,5
2
0 1 2 3
vx(m/s)
t(s)
vx=f(t)