Mouvement sur un cercle en rotation

Mécanique (d'après Mines d'Alès 1990)
A) Dans cette partie, on va déterminer la variation du champ de pesanteur terrestre avec la latitude du point
considéré à la surface de la Terre, en tenant compte de sa rotation.
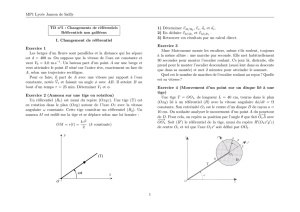
Soit un référentiel géocentrique (R), galiléen, muni d'un repère orthonormé direct (CXYZ), C est le
centre de la Terre, dont on suppose que la masse possède une répartition à symétrie sphérique de centre C.
L'axe CZ est orienté vers le pôle nord géographique.
Soit un autre référentiel (r) lié à la Terre, muni d'un repère orthonormé direct (Oxyz), en rotation
uniforme par rapport au référentiel (R). On désigne par
le vecteur rotation, supposé constant, du référentiel
(r) par rapport au référentiel (R).
Soit M(x,y,z) un point mobile dans le référentiel (r), on désigne par
v
sa vitesse et par
a
son
accélération dans (r).
+
.
S
N
C X
Z
Y
O y x
z
R
figure 1
1) Montrer que la vitesse et l'accélération de M dans le référentiel (R) sont :
V v CM
et
A a CM v
( ) 2
2) Si
G
désigne le champ de gravitation de la Terre et
g
le champ de pesanteur au même point M voisin
de O, (donc x, y et z sont très petits devant le rayon R de la Terre supposée sphérique), établir l'expression de
g
avec
G
,
et
CO
.
3) Soit la latitude nord de M, voisin de O.
a) Donner les coordonnées de
g
suivant Ox, Oy et Oz, en fonction de G, module de
G
, , module
de
, et R.

b) Soit
( , )OC g
. Donner l'expression de en fonction de , R, G et , sachant que est très
petit.
c) Calculer à la latitude = 45° nord.
On donne : G = 9,80 m.s2, R = 6,37.106 m et = 7,29.105 rad.s1.
4) Donner l'expression de la différence des modules de l'intensité de la pesanteur aux pôles et à l'équateur :
g = gpôles - géquateur.
Calculer g numériquement.
En réalité, on mesure g = 52.103 m.s2. Avancer une raison simple, en une ligne maximum, pour
expliquer l'écart observé.
B) Dans cette partie, on admettra que les coordonnées de
g
sont (0 ; 0 ; g) dans le repère (Oxyz).
1) Un point matériel M, de masse m, est abandonné sans vitesse initiale par rapport à (r), à la latitude
nord, du point de coordonnées x = 0 ; y = 0 ; z = H. Établir la loi horaire z(t) ainsi que la durée de la chute
jusqu'en O, en négligeant la force de Coriolis.
2) On ne néglige plus la force de Coriolis. Écrire les équations du mouvement. (On désignera
respectivement par
( ; ; )x y z
et
( ; ; )x y z
les coordonnées de la vitesse et de l'accélération du point M dans le
référentiel (r).
3) Le point matériel M est lâché dans les mêmes conditions qu'au B)1). Résoudre l'équation en
y
du B)2),
en prenant pour
x
et
z
les valeurs du B)1). Donner la loi horaire y(t). En prenant pour la durée de la chute la
valeur du B)1), donner l'expression de y() en fonction de , g, H et .
Calculer y() connaissant : g = 9,80 m.s2 ; = 45° nord ; H = 100 m ; = 7,29.105 rad.s1.
4) On lance un corps de masse m depuis le point O, verticalement, vers le haut, avec une vitesse initiale de
module v0.
a) Réécrire le système en
x
,
y
et
z
. Intégrer ce système pour en déduire y(t) et z(t) en utilisant les
valeurs de
x
,
y
et
z
correspondant au cas où on lance ce corps vers le haut, depuis le point O, avec une vitesse
de module initial v0, mais en négligeant la force de Coriolis.
b) Déterminer l'altitude maximale h atteinte par le corps à partir de z(t), en fonction de v0 et g.
c) Déduire du B)4)a) l'expression de y lorsque le corps retombe sur le plan (Oxy) en fonction de ,
v0, g et .
C) Dans cette partie, on désire étudier le mouvement d'un pendule simple dans le référentiel (r) lié à la
Terre. On prendra encore (0 ; 0 ; g) pour les coordonnées de
g
dans le repère (Oxyz).
1) Un pendule pesant simple, de longueur L = PM, est attaché au point P(0 ; 0 ; L) dans (r).
Au point M(x,y,z) est attachée une masse ponctuelle m. La force de tension exercée par le fil sur la
masse ponctuelle est notée
T
. À un instant donné le pendule oscille dans un plan quelconque.

z
M(x,y,z)
P(0,0,L)
y
x
O
T
figure 2
a) On pose
uMP
L
. Donner les trois coordonnées du vecteur unitaire
u
dans (r).
b) On pose
T
= T
u
. Exprimer les trois coordonnées de
T
dans (r) avec T, x, y et L, en admettant
que z << L.
2) a) En notant
x
,
y
et
z
les coordonnées de l'accélération de M dans (r), écrire les trois équations
du mouvement en fonction de x, y, R, g et L, en négligeant la force de Coriolis.
b) En admettant que
z
= 0, en déduire les deux équations simples vérifiées par
x
et
y
. On posera
02
g
L
dans ces deux équations.
3) a) En ajoutant les effets de la force de Coriolis aux équations obtenues au C)2)b), écrire les
équations en
x
et
y
, en prenant pour coordonnées de la vitesse dans (r) :
x
,
y
et
z
0
.
b) Poser = x + i y (avec i2 = 1) et écrire l'équation différentielle vérifiée par . ( On posera
x iy
et
x i y
).
4) On désire obtenir les équations du mouvement du point M dans le repère (Ox'y'z'), d'axe Oz' confondu
avec Oz et tournant autour de Oz' à la vitesse angulaire constante
= - sin
uz
On fait donc le changement
de variables = ' eit où ' = x' + i y'.
x
x'
y
y'
figure 3

a) Écrire l'équation différentielle vérifiée par ' (on notera
' ' 'x iy
et
' ' 'x i y
les dérivées
première et seconde de ' par rapport au temps).
b) Négliger le terme en 2 devant celui en 02 dans l'équation du C)4)a). Écrire alors la solution
générale '(t).
c) Les conditions initiales sont, à t = 0 : x = x0 ; y = 0 ;
x
= 0 et
y
= 0. En déduire les valeurs
initiales '0 et
'0
de ' et
'
.
d) Déduire de '(t) les expressions de x'(t), sous la forme a cos(0t), et de y'(t), sous la forme b
sin(0t); donner les expressions de a et de b, avec x0, , et 0.
e) En déduire que dans (Ox'y'z') la trajectoire de M est une ellipse. Calculer numériquement le
rapport
b
a
à la latitude = 45° nord.
On donne : g = 9,80 m.s2 ; = 7,29.105 rad.s1 et L = 67 m.
Le résultat trouvé implique que le mouvement du pendule a pratiquement lieu dans le plan (Ox'z').
Calculer b si x0 = 3 m.
f) Déduire du C)4)b) que dans (r) le plan d'oscillation du pendule tourne à la vitesse angulaire
et
calculer la période de rotation du plan d'oscillation du pendule dans (r) à la latitude de 45° nord.
1
/
4
100%