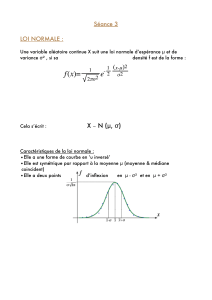
chapitre 2 : serie statistique a un caractere

CHAPITRE 2 : SERIE STATISTIQUE A UN
CARACTERE.
A) Généralités.
1) Introduction
La statistique est une méthode « scientifique » de l’information dont la matière principale
est fournie par des données numériques en nombre suffisamment important.
Ces données numériques doivent être présenter sous des formes facilement interprétables et
exploitables.
Pour ce faire, la statistique descriptive utilise :
- soit des tableaux
- soit différents types de représentation graphique
- soit des résumés numériques appelés caractéristiques.
2) Définitions et vocabulaire.
Population statistique : C’est l’ensemble des éléments à partir duquel les données sont
obtenues.
Individu en unité statistique : C’est l’élément de la population.
Echantillon : C’est une partie de la population constituée de
n
individus extraits des
conditions déterminées.
Caractère : Chaque individu de la population est repéré ou analysé selon un critère appelé
caractère.
Modalité : Chaque caractère peut présenter plusieurs états appelés modalités et les modalités
d’un caractère sont incompatibles et exhaustives.
Caractères qualitatifs : Les modalités ne sont pas mesurables même si parfois on peut les
représenter par des codes numériques.
Caractères quantitatifs : appelés aussi variables statiques lorsque les modalités sont
mesurables.
- La variable est dite « discrète » si les valeurs prises sont isolées.
- La variable est dite « continue » si les prises appartiennent a un intervalle de .
Exemple de base : Une enquête sociologique a été menée par un organisme auprès de 100
familles vivants dans une cité. Trois questions ont été posées :
- La Catégorie Socioprofessionnelle (CSP) du chef de ménage (employé, courrier,
cadre moyen, personne non-active.)
- Nombres moyens d’appareils électroménagers par famille.
- Le niveau d’endettement annuel par famille.

Dans cet exemple, les caractères sont les différentes questions de l’enquête. La détermination
dépend du caractère étudié.
Population
Unité
statistique
Caractère
Nature du
caractère
Modalités
Question 1
Ensemble des
chefs de
ménage.
UN chef de
ménage.
CSP
Qualitatif
4
(ouvrier,
employé,
cadre moyen)
Question 2
Ensemble des
familles
UNE famille
Nombre
d’appareils
électroménagers
Quantitatif,
Variable
statique
discrète
8
(0,1,2,3,
4,5,6,7)
Question 3
Ensemble des
familles
UNE famille
Niveau
d’endettement
Quantitatif,
Variable
statique
continue
6
[0,1000[ ;
[1000,2000[
[2000,2500[
[2500,3500[
[3500,4000[
[4000,5000[
B) Série Statistique a un caractère
I) Distribution statistique :
Par la suite, on considère que la population a un effectif total égal à
n
,et le caractère
analyse admet exactement
r
modalités.
1) Définition 1 :
On appelle « distribution statistique » la donnée de tous les couples
, ; 1,...,
ii
m n i r
Où
i
m
est la modalité de rang
i
et
i
n
le nombre de fois que celle-ci a été observée.
On dit que
i
n
est « l’effectif » ou la « fréquence absolue » de la
ème
i
modalité.
Propriété : L’effectif total
n
est la somme de tous les effectifs, c’est a dire :
12
...
r
n n n n   
2) Définition 2 :
On appelle « fréquence » ou « fréquence relative » de la
ème
i
modalité
i
n
la quantité notée
i
f
définie par :
i
in
fn
.
Propriétés :
01
i
f
Et
11
r
i
if
.

3) Tableaux des fréquences.
a) 1er Cas : Caractère qualitatif.
Exemple 1 : Répartition des chefs de ménage selon leur catégorie socioprofessionnelle (CSP).
CSP
ni
i
f
(en %)
Employés
30
30
Ouvriers
40
40
Cadre moyen
20
20
Non actifs
10
10
Total
100
100
b) 2ème Cas : Caractère quantitatif, variable discrète.
Exemple 2 : Nombre moyens d’appareils électroménagers par famille.
i
x
ni
i
f
0
2
0.02
1
15
0.15
2
30
0.30
3
20
0.20
4
15
0.15
5
10
0.10
6
5
0.05
7
2
0.02
Total
100
1
c) 3ème Cas : Caractère quantitatif, variable continue.
Les modalités sont des intervalles de appelés « classes » et notées
i
C
.
1
, 1,......, 1
i i i i
C où i r
représente les extrémités des classes.
Exemple 3 : Distribution du niveau d’endettement annuel de chaque famille.
Ci
ni
i
f
[0,1000[
26
0.26
[1000,2000[
30
0.30
[2000,2500[
22
0.22
[2500,3500[
14
0.14
[3500,4000[
6
0.06
[4000,5000[
2
0.02
Total
100
1

d) Fréquence cumulées.
Définition : On appelle « fréquence cumulée » de la
ème
i
modalité d’une variable statistique,
la somme des fréquences des
i
premières modalités.
On la note par
i
F
et on a :
12 1
... i
i i j
j
F f f f f
Propriétés :
1
F
=
1
f
11
r
ri
i
Ff
4) Fonction de répartitions .
Définition : on appelle fonction de répartition d’une distribution statistique, l’application F
qui à tout nombre réel
x
associe la proportion d’individus, dont le caractère est
strictement inférieur à
x
.
Propriétés : a) F(
x
1) = 0 ( Cas discret )
Et F(
1) = 0 ( Cas continu )
b) Pour tout
x
contenu dans l’intervalle ]
x
k ,
x
k+1] ( avec
x
k <
x
≤
x
k+1 ), on a:
a. F(
x
)=
1f
+
2f
+……+
kf
=
1
k
i
if
()kF
( Cas discret )
b.
k 1 2 1) .....(kf f fF  
( 1)
1
1k
k
i
ifF
( Cas continu )
Remarque : Pour tout
1,]kkxxx 
, si on fait tendre
x
vers
1kx
, alors :
1
11
( ) ( )lim kk
k
k
i
xx i
F x F f Fx
 Donc F est une fonction continue a gauche.
c.
( ) 0F 
et
( ) 1F 

Exemple numérique : Cas discret : (Tableau de l’exemple 2).
xi
ni
fi
Fi
F(
x
)
0
2
0.02
2
0
1
15
0.15
17
0.02
2
30
0.30
47
0.17
3
20
0.20
67
0.47
4
15
0.15
82
0.67
5
10
0.10
92
0.82
6
5
0.05
97
0.92
7
3
0.03
100
0.97
Total
100
1
1
Interprétation : - Par exemple, 67% des familles ont au plus 3 appareils
électroménagers, car F(4) = 0.67
- Ou alors 98% des familles possèdent au moins 1 appareil
électroménager, car F(1) = 0.02
Cas continu : (Tableau de l’exemple 3).
i
ni
i
f
Fi (en %)
F(
x
)
0
---------------------
---------------------
---------------------
0
26
26
26
1000
---------------------
---------------------
---------------------
0.26
30
30
56
2000
---------------------
---------------------
---------------------
0.56
22
22
78
2500
---------------------
---------------------
---------------------
0.78
14
14
92
3500
---------------------
---------------------
---------------------
0.92
6
6
98
4000
---------------------
---------------------
---------------------
0.98
2
2
100
5000
---------------------
---------------------
---------------------
1
Total
100
100
Interprétation : Par exemple, 78% des familles ont des niveaux d’endettement supérieur ou
égal a 2500, car F(2500) = 0.78