A. Problème de conditions initiales

I. Intégration numérique
A. Problème de conditions initiales
Soient un intervalle
b;a
fermé de R, une application f :
RRR 
, et une application différentiable y :
RR 
. On
considère le problème-type suivant (problème de Cauchy) :
)x(y,xf)x('y 
;
b;ax
avec
0
y)a(y 
(condition
initiale)
(f est une fonction donnée, y une fonction inconnue à déterminer ;
Ry0
donné).
1. Méthodes à pas séparés
a) Méthodes de type Euler
On subdivise l'intervalle d'intégration
b;a
en N sous-intervalles de longueur égale
Nab
h
, délimités par les points de subdivision
hnaxn
,
1N;...;1;0n 
.
Pour chaque abscisse
n
x
, on calcule une valeur approchée
n
y
de la vraie valeur
)x(y n
de la fonction y.
 Euler
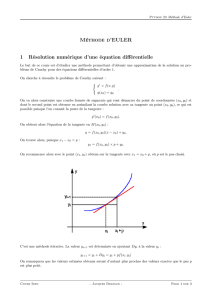
Pour cela, on considère la tangente en
nn y;x
à la courbe intégrale passant par ce point. La valeur de
1n
y
est l'ordonnée du point de
cette droite d'abscisse
1n
x
. On applique donc :
nnn1n y;xfhyy 
1N;...;1;0n 
 Euler amélioré
Pour cela, on remplace dans la formule d’Euler la pente de la tangente
nn y;xf
par la valeur corrigée au milieu de l'intervalle
1nn x;x 
. On applique donc :
nnnnn1n y;xf
2
h
y;
2
h
xfhyy
1N;...;1;0n 
 Euler-Cauchy
Pour cela, on remplace dans la formule d’Euler la pente de la tangente
nn y;xf
par la moyenne de cette pente avec la valeur corrigée
en
1n
x
. On applique donc :
nnnnnnn1n y;xfhy;hxfy;xf
2
h
yy 
1N;...;1;0n 

b) Runge-Kutta
La méthode de Runge-Kutta peut être considérée comme une généralisation des méthodes de type Euler. Elle est définie par :
)x(yy
h;y;xhyy
00
nnn1n
Pour la méthode d’Euler, on a
f
. L'objectif est d'obtenir une meilleure précision grâce au degré de liberté supplémentaire que
constitue le choix de la fonction .
Avant de rentrer dans les détails de cette méthode, il nous définir la notion d’ordre. Ainsi, dans le cas présent, une méthode à 1 pas est
d’ordre p si et seulement si :
p
nn
p
nn
n1n hK'yx'yhKh;xy;x
hxyxy 
où K ne dépend que de y et de f.
Pour ce type de méthode, on peut montrer que l’erreur commise, i.e. , l’écart
n
e
à la vraie solution :
p
nnn hOy)x(ye 
.
Les méthodes de Runge-Kutta propagent une solution sur un intervalle en combinant les informations provenant de plusieurs pas de calculs
de type de ceux mis en œuvre dans le processus de Euler. Ces informations servent à apparier un développement de Taylor au voisinage de la
solution jusqu'à un ordre plus élevé que celui obtenu par les processus de Euler. A titre d’exemple, détaillons les calculs pour une méthode
d'ordre 2 :
Soit une fonction f. Par le développement de Taylor, on obtient :
)h(o)x(y
6
h
)x("y
2
h
)x('yh)x(y)hx(y 3)3(
32
Donc :
)h(o)x(y
6
h
)x("y
2
h
)x('y
h)x(y)hx(y 2)3(
2
or :
)x(y,xf)x('y 
Donc :
)x(y,xf
y
)x('y)x(y,xf
x
)x("y 
Soit :
)x(y,xf
y
)x(y,xf)x(y,xf
x
)x("y 
Posons :
)x(y,xf
y
)x(y,xf)x(y,xf
x
)x(y,xf )1(
Il vient :
)h(o)x(y
6
h
)x(y,xf
2
h
)x(y,xf
h)x(y)hx(y 2)3(
2
)1( 
On choisit :
)x(y,xf
2
h
)x(y,xfh);x(y;x )1(
Donc :
)h(o)x(y
6
h
h);x(y;x
h)x(y)hx(y 2)3(
2
Autrement dit :
)h(Oh);x(y;x
h)x(y)hx(y 2

Pour cette fonction on a obtenu une meilleure précision. Cependant, cette fonction est difficile à évaluer car il faut les dérivées de f par
rapport à x et y. C'est pourquoi on cherche ne dépendant que de f et pas de ses dérivées. Pour cela, on recherche de la forme :
y;xfhy;hxfay;xfah;y;x 21 
Il faut donc déterminer les 4 paramètres
 et ,a,a 21
pour conserver une précision d'ordre 2. Pour cela, on repart de
)h(o)x(y
6
h
)x("y
2
h
)x('y
h)x(y)hx(y 2)3(
2
)h(O)y,xf
2
h
y,xf
h)x(y)hx(y 2)1( 
Par développement de Taylor,
y
f
h
x
f
hfy;xfhy;hxf 
)h(o
yf
y
f
x
f
2
xf
2
h2
2
2
2
2
2
2
2
En ne gardant que les termes de premier ordre, on finit par obtenir :
)h(Of
y
f
a
x
f
ahy;xf)aa(h;y;x 2
2221 
Donc :
 h);x(y;x
h)x(y)hx(y
)h(Of
y
f
a
2
1
x
f
a
2
1
hf)aa1( 2
2221 
On souhaite que le terme de droite se réduise à
)h(O 2
. On peut donc en déduire les valeurs des paramètres :
a21
aa
2
1
a
2
1
a
1aa
2
2
2
21
La solution n'étant pas unique (le paramètre a est indéterminé), on aboutit à une famille de méthodes de la forme :
 y;xf
a2h
y;
a2h
xfay;xf)a1(h;y;x
Remarques
a = 1 correspond à la méthode d’Euler modifiée
a =
2
1
correspond à la méthode d’Euler-Cauchy, connue également sous le nom de méthode de Henn

Dans la pratique, on utilise plus souvent la méthode de Runge-Kutta d'ordre 4 dont l'erreur est
)h(O 4
. La recherche de
la fonction se fait de la même manière que pour l'ordre 2 mais en beaucoup plus complexe!! On arrive à :
4321nn
nnn1n
kk2k2k
6
1
h;y;x
h;y;xhyy
avec :
3nn4
2nn3
1nn2
nn1
khy;hxfk
k
2
h
y;
2
h
xfk
k
2
h
y;
2
h
xfk
y;xfk
L’avantage d’une telle méthode est que l’on peut relativement facilement mettre en place une stratégie d’intégration à pas
variable.
Pourquoi ? Il est relativement clair que plus le pas sera petit, meilleure sera l’approximation de la courbe intégrale.
Néanmoins, il faut garder à l’esprit qu’un calcul se doit d’être efficace. Ainsi, si l’intervalle d’intégration est grand, il est
opportun de mettre en place une technique permettant d’augmenter ce pas.
Soient l’équation différentielle
)x(y,xf)x('y 
,
h;y;x nn4
et
h;y;x nn5
les fonctions
correspondant respectivement aux méthodes de Runge-Kutta d’ordre 4 et 5. Supposons maintenant qu’on ait intégré notre
équation jusqu’au point
nn y;x
par la méthode d’ordre 4 et calculons :
h;y;xhy)x(yh;y;xhy)x(y nn
5
n1nnn
4
n1n  
h;y;xhh;y;xh nn
5
nn
4
=E
h;y;xhy)x(yh;y;xhy)x(y nn
5
n1nnn
4
n1n  
54 hO)h(O 
Ce qui revient à dire que l’on est capable de calculer l’erreur que l’on commet à chaque pas. Donc, on peut envisager ce
schéma : En
nn y;x
, on double le pas en cours (h = 2.h), on calcule E. Si (E) est supérieur à une précision que l’on
s’est fixée initialement ( ), on conserve cette nouvelle valeur du pas. Sinon, on le divise le pas par 2 jusqu’à ce que E soit
inférieur à .

2. Méthodes à pas liés
a) Nyström
On subdivise l'intervalle d'intégration
b;a
en N sous-intervalles de longueur égale
Nab
h
, délimités par les points de subdivision
hnaxn
,
1N;...;1;0n 
. Pour chaque abscisse
n
x
, on calcule une valeur approchée
n
y
de la vraie valeur
)x(y n
de la fonction y.
Pour cela, on considère la droite de pente
nn y;xf
passant par le point
1n1n y;x 
. Cette droite est parallèle à la tangente à la
courbe intégrale passant par
nn y;x
. La valeur de
1n
y
est l'ordonnée du point de cette droite d'abscisse
1n
x
.
On applique alors pour le calcul du premier point une méthode à pas lié (présentée plus haut), puis :
nn1n1n y;xfh2yy  
1N;...;2;1n 
b) Euler implicite
On subdivise l'intervalle d'intégration
b;a
en N sous-intervalles de longueur égale
Nab
h
, délimités par les points de subdivision
hnaxn
,
1N;...;1;0n 
. Pour chaque abscisse
n
x
, on calcule une valeur approchée
n
y
de la vraie valeur
)x(y n
de la fonction y.
Pour cela, on considère la droite de pente
nn y;xf
passant par le point
nn y;x
; Cette droite est parallèle à la tangente à la courbe
intégrale passant par
1n1n y;x 
. La valeur de
1n
y
est l'ordonnée du point de cette droite d'abscisse
1n
x
. On applique alors :
1nnn1n y;xfh2yy  
1N;...;1;0n 
C'est une équation en
1n
y
qu'il faut résoudre à l'aide d'une méthode numérique.
yn+1
yn
yn-1
xn+1 xn xn-1
yn+1
yn
yn-1
xn+1 xn xn-1