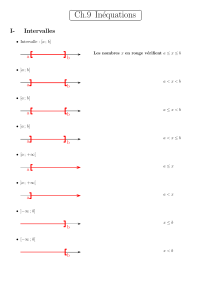
Equations et inéquations

Coll` ege Calvin 2015 – 2016
Equations et in´ equations
ALG` EBRE 2MA
1 Introduction
Dans ce chapitre, nous nous pencherons sur des r´ esultats et des techniques portant sur la r´ esolution de divers
types d’´ equations et d’in´ equations alg´ ebriques nouvelles, dont certaines sont en lien avec les notions de G´ eom´ e-
trie Analytique vues au chapitre pr´ ec´ edent et d’autres nous fournirons des outils math´ ematiques utiles ` a l’´ etude
des fonctions abord´ ees dans le chapitre suivant.
2 Equations irrationnelles
Les ´ equations dites irrationnelles sont des ´ equations comportant des termes o` u intervient un radical (ou racine),
c’est-` a-dire une op´ eration du type n
√A, avec n∈N∗, pour Aune expression alg´
ebrique ` a valeur dans R. Un
exemple d’´ equation de ce type serait l’´ equation suivante
2x−1=2+√x+6.(1)
Comme des nombres r´ eels tels que √2,3
√−5,4
√7sont irrationnels, c’est-`
a-dire ne peuvent s’´ ecrire sous la
forme a
b, avec a∈Zet b∈Z∗, on d´
esigne par analogie ces ´ equations par l’´ epith` ete d’irrationnelles.
2.1 Technique de r´ esolution
La strat´ egie pour r´ esoudre une ´ equation telle que (1) consiste ` a proc´ eder comme suit :
i. isoler la racine ;
ii. ´ elever chaque membre ` a la puissance inverse de la racine ;
iii. r´ esoudre l’´ equation obtenue ;
iv. dans le cas de racines paires,v
´
erifier que les solutions obtenues au point iii. satisfont l’´ equation de
d´ epart.
Remarque. Le point iv. est n´ ecessaire, car en ´ elevant une ´ equation ` a une puissance paire, celle-ci peut
admettre des solutions suppl´ ementaires, qui ne sont pas solutions de l’´ equation de d´ epart.
Exemples illustrant le point iv.
Consid´ erons l’´ equation du premier degr´ e:
2x=x+1.(2)
Si l’on la r´ esout, on trouve une solution unique :
2x=x+1 ⇐⇒ x=1 ⇐⇒ S={1}.
•Si maintenant on ´ el` eve au carr´ echaque membre de l’´ equation (2) et qu’on r´ esout cette nouvelle ´ equation,
on obtient deux solutions distinctes.
(2x)2=(x+ 1)2⇐⇒ 4x2=x2+2x+1 ⇐⇒ 3x2−2x−1=0 (3)
1

⇐⇒ x±=2±√16
6⇐⇒ S=−1 3;1
.
On observe que seul x=1est solution de l’´ equation de d´ epart. La valeur x=1
3est solution de
l’´ equation quadratique (3), mais non de l’´ equation du premier degr´ e initiale (2).
•En revanche si l’on ´ el` eve l’´ equation (2) au cube et qu’on r´ esout cette nouvelle ´ equation, on obtient le
mˆ eme nombre de solution qu’initialement.
(2x)3=(x+ 1)3⇐⇒ 16x3=x3+3x2+3x+1 ⇐⇒ 15x2−3x2−3x−1=0
⇐⇒ (x−1)
⇒x=1 7x2+4x+1
∆=−12<0
=0 ⇐⇒ S={1}.
Remarque
La raison pour laquelle ´ elever une ´ equation ` a une puissance impaire ne change pas le nombre de solution de
celle-ci provient du fait que, comme nous le verrons plus tard, les fonctions du type x→ x2n+1,n∈N, sont
des bijections de Rdans R, c’est-` a-dire qu’elles font correspondre ` a tout ´ el´ ement de l’ensemble d’arriv´ ee yun
et un seul ´ el´ ement de l’ensemble de d´ epart x. Elever une ´ equation ` a une puissance impaire conserve ainsi le
nombre (et la valeur) des solutions, par rapport ` a l’´ equation de d´ epart.
Des fonctions du type x→ x2n,n∈N, ne sont pas des bijections, c’est-` a-dire en particulier qu’elles
peuvent faire correspondre ` a un yplusieurs xdiff´ erents. Ceci permet d’expliquer pourquoi lorsqu’on ´ el` eve une
´
equation ` a une puissance paire, l’´ equation obtenue peut admettre plus de solutions que l’´ equation initiale.
2.2 Mod` eles de r´ esolution d’´ equations irrationnelles
2

3

Exercice 1.
R´ esoudre dans Rles ´ equations irrationnelles suivantes.
1) x−√x−2=0,4) √3x+1=1−x, 7) √x+4+√x+7=3,
2) 1
√x=2
x−1,5) 3 −√1−2x=x, 8) √2x+3−√x+1=1,
3) 2 + 3
√1−5t=0,6) 5
√2x2+1−2=0,9) 5√x=√2x−3.
Exercice 2.
a)
b)
4

3 In´ equations du premier degr´ e` a une inconnue
Commenc¸ons par un exemple.
Probl` eme. On cherche ` ar
´
esoudre l’in´ equation suivante
2(x−4) ≤1
2x+3 .(4)
Cette in´ equation contient une inconnue au premier degr´ e(x). Elle comporte un membre de gauche et un
membre de droite, s´ epar´ es par un signe d’in´ egalit´ e : ≤.
Remarque 1. R´ esoudre l’in´ equation (4) consiste ` a trouver toutes les valeurs de l’inconnue qui v´ erifient
l’in´ egalit´ e. Ces valeurs sont appel´ ees les solutions de l’in´ equation. On d´ esignera par Sl’ensemble de ces
solutions.
Remarque 2. Lorsqu’on r´ esout une in´ equation ou un syst` eme d’in´ equations, l’ensemble des solutions Sest
en g´ en´ eral un intervalle.
3.1 Propri´ et´ es des in´ egalit´ es
Afin de r´ esoudre une in´ equation, on a recours aux PROPRI ´ ET´ ES des in´ egalit´ es suivantes, qui permettent de
transformer l’in´ egalit´ e en une in´ egalit´ e´ equivalente de la forme : x>a(x≥a) ou x<b(x≤b), avec aet b
des nombres r´ eels.
PROPRI ´ ET´ ES DES IN´ EGALIT´ ES
(P1) Propri´ et´ e1:Additivit´ e.
On peut ajouter (ou retrancher) un mˆ eme nombre ` a chaque membre d’une in´ egalit´ e, sans en changer le
sens. Soient deux nombres a, b ∈R.
∀c∈R:si a≤b, alors a+c≤b+c.
Exemple
Consid´ erons l’in´ egalit´ e:7<8. Si l’on ajoute (−2) ` a chaque membre, on a bien : 7−2<8−2(car
en effet : 5<6).
(P2) Propri´ et´ e2:Multiplication par un nombre positif.
On peut multiplier (ou diviser) chaque membre d’une in´ egalit´ e par un mˆ eme nombre positif, sans
changer le sens de l’in´ egalit´ e. Soient trois nombres a, b, c ∈R.
∀c>0: si a≤b, alors a·c≤b·c.
Exemple
Consid´ erons l’in´ egalit´ e:7<8. On peut multiplier chaque membre par 3, sans changer le sens de
l’in´ egalit´ e:3·7<3·8(car en effet : 21 <24).
(P3) Propri´ et´ e3:Multiplication par un nombre n´ egatif.
On peut multiplier (ou diviser) chaque membre d’une in´ egalit´ e par un mˆ eme nombre n´ egatif, ` a condi-
tion de changer le sens de l’in´ egalit´ e. Soient trois nombres a, b, c ∈R.
∀c<0: si a≤balors a·c≥b·c.
Exemple
Consid´ erons l’in´ egalit´ e:7<8. On peut multiplier chaque membre par (−1),` a condition de changer
le sens de l’in´ egalit´ e:(−1) ·7>(−1) ·8(car en effet : −7>−8).
5