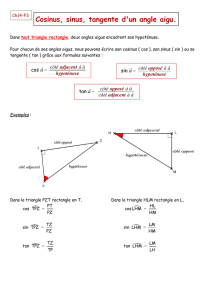
Chapitre 9 Fonctions trigonométriques

Chapitre 9
Fonctions trigonom´etriques
9.1 D´efinitions et repr´esentations graphiques
9.1.1 Fonctions cosinus et sinus
D´efinition 9.1
Soit P(1; 0) sur le cercle trigonom´etrique. Soit encore
M, l’image de Ppar une rotation de centre Oet
d’angle α.
On appelle cosinus de l’angle α, not´e cos(α), la
premi`ere coordonn´ee ou abscisse de M. Celle-ci cor-
respond `a la mesure alg´ebrique du segment OC, o`u
Cest la projection de Msur l’axe des abscisses.
On appelle sinus de l’angle α, not´e sin(α), la seconde
coordonn´ee ou ordonn´ee de M. Celle-ci correspond
`a la mesure alg´ebrique du segment OS, o`u Sest la
projection de Msur l’axe des ordonn´ees.
x
y
I
J
α
M
C
S
O
sin(α)
cos(α)
On note : M(cos(α),sin(α))
Repr´esentations graphiques
En g´en´eral, le radian sera utilis´e comme unit´e de mesure (sauf indication contraire).
Ainsi, si on parle de la fonction f(x) = sin(x), il est entendu que xest exprim´e en
radians. Les calculatrices doivent donc ˆetre convenablement configur´ees pour travailler
avec les fonctions trigonom´etriques.
La repr´esentation graphique de la fonction cosinus :
cos : R−→ [−1; 1]
x7−→ cos(x)
est donn´ee ci-dessous.
102

Math´ematiques, MAT-MAB-MAP 1`ere ann´ee 9. Fonctions trigonom´etriques
π
2π3π
22π5π 23π
−π
2
−π
−3π
2
−2π
−5π
2
−3π
1
−1
x
y
y= cos(x)
La repr´esentation graphique de la fonction sinus :
sin : R−→ [−1; 1]
x7−→ sin(x)
est donn´ee ci-dessous.
π
2π3π
22π5π 23π
−π
2
−π
−3π
2
−2π
−5π
2
−3π
1
−1
x
y
y= sin(x)
Propri´et´es
La fonction cosinus poss`ede les propri´et´es suivantes :
– son ensemble de d´efinition est Dcos =R.
– son ensemble image est l’intervalle [−1; 1].
– elle est une fonction paire car pour tout x∈ Dcos on a cos(−x) = cos(x).
– elle est une fonction born´ee.
La fonction sinus poss`ede les propri´et´es suivantes :
– son ensemble de d´efinition est Dsin =R.
– son ensemble image est l’intervalle [−1; 1].
– elle est une fonction impaire car pour tout x∈ Dsin on a sin(−x) = −sin(x).
– elle est une fonction born´ee.
9.1.2 Les fonctions tangente et cotangente
D´efinition 9.2
Soit M(cos(α),sin(α)) sur le cercle trigonom´etrique.
On d´efinit le point Tcomme l’intersection entre la droite passant par (0; 0) et Met la
droite verticale tangente au cercle au point I(1; 0).
On d´efinit encore le point Kcomme l’intersection entre la droite passant par (0; 0) et M
(la mˆeme que ci-dessus) et la droite horizontale tangente au cercle au point J(0; 1).
page 103

Math´ematiques, MAT-MAB-MAP 1`ere ann´ee 9. Fonctions trigonom´etriques
On appelle tangente de l’angle α, not´e tan(α),
l’ordonn´ee de T. Celle-ci correspond `a la mesure
alg´ebrique du segment IT .
On appelle cotangente de l’angle α, not´e cot(α),
l’abscisse de K. Celle-ci correspond `a la mesure
alg´ebrique du segment JK.
On note : T(1; tan(α)) et K(cot(α); 1)).
x
y
I
J
α
M
K
T
O
tan(α)
cot(α)
Remarques
1. Lorsque la droite passant par (0; 0) et Mest verticale, la tangente de l’angle correspon-
dant n’est pas d´efinie (il n’y a pas de point d’intersection comme les deux droites sont
verticales). Ceci se produit pour les angles de l’ensemble {x∈R|x=π
2+kπ, k ∈Z}.
2. Lorsque la droite passant par (0; 0) et Mest horizontale, la cotangente de l’angle
correspondant n’est pas d´efinie (il n’y a pas de point d’intersection comme les deux
droites sont horizontales). Ceci se produit pour les angles de l’ensemble {x∈R|x=
kπ, k ∈Z}.
Repr´esentations graphiques
La repr´esentation graphique de la fonction tangente :
tan : R\ {x∈R|x=π
2+kπ, k ∈Z} −→ R
x7−→ tan(x)
est donn´ee ci-dessous.
π
2π3π
22π5π 23π
−π
2
−π
−3π
2
−2π
−5π
2
−3π
1
−1
x
y
y= tan(x)
La repr´esentation graphique de la fonction cotangente :
cot : R\ {x∈R|x=kπ, k ∈Z} −→ R
x7−→ cot(x)
est donn´ee ci-dessous.
page 104

Math´ematiques, MAT-MAB-MAP 1`ere ann´ee 9. Fonctions trigonom´etriques
π
2π3π
22π5π 23π
−π
2
−π
−3π
2
−2π
−5π
2
−3π
1
−1
x
y
y= cot(x)
Propri´et´es
La fonction tangente poss`ede les propri´et´es suivantes :
– son ensemble de d´efinition est Dtan =R\ {x∈R|x=π
2+kπ, k ∈Z}.
– son ensemble image est l’ensemble des nombres r´eels, R.
– elle est une fonction impaire car pour tout x∈ Dtan on a tan(−x) = −tan(x).
– elle est une fonction non born´ee.
La fonction cotangente poss`ede les propri´et´es suivantes :
– son ensemble de d´efinition est Dcot =R\ {x∈R|x=kπ, k ∈Z}.
– son ensemble image est l’ensemble des nombres r´eels, R.
– elle est une fonction impaire car pour tout x∈ Dcot on a cot(−x) = −cot(x).
– elle est une fonction non born´ee.
9.1.3 Fonctions p´eriodiques
En consid´erant les figures qui nous ont permis de d´efinir les fonctions cosinus, sinus,
tangente et cotangente, on constate que l’ajout `a l’angle αd’un multiple entier de 2πne
change pas le point Msur le cercle trigonom´etrique. De mˆeme, l’ajout `a l’angle αd’un
multiple entier de πne change pas le point T, ni le point K.
De mˆeme, sur les repr´esentations graphiques, on remarque que, en ”d´ecalant” la fonction
sinus ou cosinus de 2πvers la droite ou vers la gauche, elle ne se modifie pas (le dessin reste
le mˆeme). La mˆeme observation peut ˆetre faite pour les fonctions tangente et cotangente
avec un d´ecalage de π.
Ainsi, par d´efinition des fonctions trigonom´etriques, on a
cos(α+k·2π) = cos(α),∀k∈Z
sin(α+k·2π) = sin(α),∀k∈Z
tan(α+k·π) = tan(α),∀k∈Z
cot(α+k·π) = cot(α),∀k∈Z
On dit que les fonctions sinus et cosinus sont p´eriodiques de p´eriode 2πet que les
fonctions tangente et cotangente sont p´eriodiques de p´eriode π.
page 105

Math´ematiques, MAT-MAB-MAP 1`ere ann´ee 9. Fonctions trigonom´etriques
Remarques
1. Pour les fonction sinus et cosinus, le nombre krepr´esente le nombre de tours entre
deux angles ayant, respectivement, le mˆeme sinus ou le mˆeme cosinus.
2. Pour les fonction tangente et cotangente, le nombre krepr´esente le nombre de demi-
tours entre deux angles ayant, respectivement, la mˆeme tangente ou la mˆeme cotan-
gente.
Plus g´en´eralement, on a la d´efinition suivante.
D´efinition 9.3
Une fonction fde D(D⊂R) vers Rest p´eriodique s’il existe p∈R∗
+, tel que, pour
tout x∈D, on a
a) x+p∈D
b) f(x+p) = f(x)
Le plus petit nombre r´eel strictement positif psatisfaisant cette condition est appel´e la
p´eriode de f. Pour tout multiple entier kp (k∈Z) de p, on a :
x+kp ∈Det f(x+kp) = f(x)∀x∈D.
La connaissance du graphe de frestreinte `a un intervalle de longueur ppermet de
repr´esenter le graphe de fsur Dtout entier, grˆace `a des translations dans la direction
de l’axe Ox.
9.1.4 Fonctions sinuso¨ıdales
D´efinition 9.4
Une fonction fest dite sinuso¨ıdale s’il existe quatre nombres nombres r´eels a,b,cet d,
tel que :
f(x) = a·sin(b·(x−c)) + d
On appelle al’amplitude et cle d´ephasage.
Exemple
Le graphique de la fonction sinuso¨ıdale f(x) = 3
2·sin (2(x−π)) + 1 est donn´ee
ci-dessous.
π
2π3π
22π5π 23π
−π
2
−π
−3π
2
−2π
−5π
2
−3π
1
−1
x
y
y=f(x)
Effets des param`etres a,b,cet d
Durant les exercices, nous donnerons une interpr´etation des effets des param`etres a,b,c
et ddans le cas d’une fonction sinuso¨ıdale en se basant sur les repr´esentations graphiques
de quelques fonctions r´ealis´ees sur papier millim´etr´e.
page 106