Dimension d`un espace vectoriel. Exemples et applications.

Dimension d’un espace vectoriel. Exemples et applications.
Par Nicolas Lanchier 1
1. Th´eorie de la dimension.
Dans toute la suite, Kd´esigne un corps commutatif et Eun K-espace vectoriel.
D´efinition 1.1 Une famille (xi)i∈Ide vecteurs de Eest dite libre si
X
i∈I
λixi= 0 =⇒λi= 0 ∀i∈I.
D´efinition 1.2 Une partie A⊂Eest dite g´en´eratrice si vect(A) = E. [3], Sect. 3.1
D´efinition 1.3 On appelle base du K-espace vectoriel Etoute famille (xi)i∈I⊂E`a la fois libre
et g´en´eratrice. [3], Sect. 3.1
D´efinition 1.4 On dira que Eest de dimension finie, ce que l’on supposera syst´ematiquement
par la suite, s’il existe une famille g´en´eratrice finie de E. [3], Sect. 3.1
Th´eor`eme 1.5 (base incompl`ete) Soient Gun syst`eme fini de g´en´erateurs de Eet L ⊂ G un
syst`eme libre. Alors il existe une base Bde Etelle que L ⊂ B⊂ G. [3], Sect. 3.1
Th´eor`eme 1.6 Toutes les bases de Eont mˆeme cardinal n. L’entier nainsi d´efini est appel´e
dimension de E, ce que l’on notera dim E=n. [3], Sect. 3.1
Proposition 1.7 Soient E1et E2deux sous-espaces vectoriels de E. Alors les conditions suivantes
sont ´equivalentes :
1. E=E1⊕E2.
2. dim E= dim E1+ dim E2et E1∩E2={0}.
3. dim E= dim E1+ dim E2et E=E1+E2. [3], Sect. 3.1
Th´eor`eme 1.8 (th´eor`eme du rang) Soient Fun K-espace vectoriel et f:E−→ Fune appli-
cation lin´eaire. Alors fest de rang fini et dim E= dim Ker f+ rg f. [3], Sect. 3.2
Th´eor`eme 1.9 Si Fest un sous-espace vectoriel de Ealors dim E= dim F+ dim F⊥. De mˆeme,
si Gest un sous-espace vectoriel de l’espace dual E∗alors dim E∗= dim G+ dim G◦. [3], Sect. 3.4
2. Application aux invariants de similitudes.
D´efinition 2.1 Soient Eun K-espace vectoriel de dimension finie et f∈L(E) une application
lin´eaire. Pour tout x∈E, on appelle polynˆome minimal de xrelatif `a fl’unique polynˆome unitaire
de plus bas degr´e Px∈K[X] tel que Px(f)(x) = 0. [3], Sect. 4.2
Proposition 2.2 Ex={P(f)(x) : P∈K[X]}est un espace vectoriel de dimension deg(Px). [3],
Sect. 4.2
D´efinition 2.3 Une application lin´eaire f∈L(E) est dite cyclique s’il existe x∈Etel que
E=Ex. [3], Sect. B.1
1Tout usage commercial, en partie ou en totalit´e, de ce document est soumis `a l’autorisation explicite de l’auteur.

Th´eor`eme 2.4 Etant donn´e f∈L(E), il existe une suite F1, F2,···, Frde sous-espaces vectoriels
de Estables par fet tels que
1. E=F1⊕F2⊕ ··· ⊕ Fr.
2. Pour tout 1 ≤i≤r, la restriction fide f`a Fiest un endomorphisme cyclique de Fi.
3. Si Pid´esigne le polynˆome minimal de fialors pour tout 1 ≤i≤r,Pi+1 divise Pi.
De plus, la suite P1, P2,··· , Prne d´epend que de fet non du choix de la d´ecomposition. On
l’appelle suite des invariants de similitude de f. [3], Sect. B.1
Application 2.5 (r´eduction de Frobenius) Notons P1, P2,···, Prla suite des invariants de
similitude de f∈L(E) et pour tout 1 ≤i≤r,C(Pi) la matrice compagnon de Pi. Alors il existe
une base de Edans laquelle la matrice de fest donn´ee par
A=
C(P1) 0
...
0C(Pr)
[3], Sect. B.1
3. Extensions de corps et points constructibles.
D´efinition 3.1 Le degr´e d’une extension de corps K⊂Lest ´egal `a la dimension de Lvu comme
espace vectoriel sur le corps K. Le degr´e de K⊂Lest not´e [L:K].
Th´eor`eme 3.2 (multiplicativit´e des degr´es) Soient K⊂Mune extension de corps et Lun
corps interm´ediaire entre Ket M. Alors
[M:K] = [M:L]·[L:K].
Preuve. ´ Etant donn´ees (a1, a2,...,an) une base du K-espace vectoriel Let (b1, b2,...,bm) une
base du L-espace vectoriel M, il est facile de voir que
(a1b1, a1b2, . . . , a1bm, a2b1, . . . , anb1, . . . , anbm)
est une base du K-espace vectoriel M. En notant que son cardinal est ´egal `a n×m, la conclusion
est imm´ediate. 
Th´eor`eme 3.3 Soient K⊂Lune extension de corps et aun ´el´ement de L. Alors aest alg´ebrique
sur Ksi et seulement si dimKK(a)<∞. [4], Sect. 3.1
Th´eor`eme 3.4 (Wantzel) Tout r´eel constructible est alg´ebrique sur Qde degr´e une puissance
de 2. [1], Sect. 2.22
Preuve. ´ Etant donn´e xun r´eel constructible, il existe une suite croissante A0⊂ ··· ⊂ Ande
parties de R2telles que
1. A0={O, I}.
2. Ai=Ai−1∪ {Pi}avec Piconstructible en une ´etape `a partir de Ai−1.
3. (x, 0) ∈An.

Notons alors Kile corps engendr´e par les coordonn´ees des points de Aide sorte que K0=Q
et x∈Kn. Les ´equations de droites ou de cercles ´etant de degr´e ≤2, il n’est pas difficile de
montrer que [Ki:Ki−1]≤2. La formule de multiplicativit´e des degr´es implique que
[Kn:Q] = [Kn:Kn−1]·[Kn−1:Kn−2]···[K1:Q] = 2m
= [Kn:Q(x)] ·[Q(x) : Q].
Il en r´esulte que xest alg´ebrique et que [Q(x) : Q] est une puissance de 2. 
Corollaire 3.5 Il est impossible de dupliquer un cube `a la r`egle et au compas.
Preuve. En tant que racine du polynˆome irr´eductible X3−2, le r´eel 3
√2 est alg´ebrique sur Qde
degr´e 3. Il r´esulte du th´eor`eme de Wantzel que 3
√2 n’est pas constructible `a la r`egle et au compas
d’o`u bien sˆur l’impossibilit´e de dupliquer un cube. 
Corollaire 3.6 Il est impossible de trisecter un angle `a la r`egle et au compas.
Preuve. Montrons par exemple que l’angle π/3 ne peut pas ˆetre trisect´e, i.e. que le r´eel a=
cos(π/9) n’est pas constructible. L’´equation cos 3θ= 4 cos3θ−3 cos θmontre que aest racine
du polynˆome irr´eductible 4X3−3X−1. En particulier, aest alg´ebrique de degr´e 3 donc non
constructible en vertu du th´eor`eme de Wantzel. 
Lemme 3.7 Etant donn´e Gun p-groupe d’ordre pnil existe une suite G0⊂ ··· ⊂ Gnde sous-
groupes distingu´es de Gtels que |Gi|=pipour tout 0 ≤i≤n. [2], Ex. 1.4
Th´eor`eme 3.8 Soient Lun sous-corps de Ret (x, y) un ´el´ement de L2. Si l’extension Q⊂Lest
normale de degr´e une puissance de 2 alors le point de coordonn´ees (x, y) est constructible `a la
r`egle et au compas. [2], Ex 4.14
Preuve. Soit G= Gal(L|Q) le groupe de Galois de l’extension Q⊂L. Cette extension ´etant
normale, il r´esulte du th´eor`eme de correspondance de Galois que |G|= [L:Q] = 2n. En particulier,
d’apr`es le lemme 3.7, il existe une suite G0⊂ ··· ⊂ Gnde sous-groupes distingu´es de Gtels que
|Gi|= 2ipour tout 0 ≤i≤n. Notons Ki= inv(Gn−i) le corps des invariants de Gn−isoit
Ki={x∈L:σ(x) = xpour tout σ∈Gn−i}.
Il est clair que K0=Qet Kn=L. Par ailleurs, comme (Gn−i:Gn−i−1) = 2, Gn−i−1est ´egalement
distingu´e dans Gn−i. Une nouvelle application du th´eor`eme de correspondance nous permet alors
d’affirmer que
[Ki+1 :Ki] = |Gal(Ki+1 |Ki)|= (Gn−i:Gn−i−1) = 2.
Pour conclure, montrons par r´ecurrence que les ´el´ements de Ki, 0 ≤i≤n, sont constructibles `a la
r`egle et au compas. Tout d’abord, la constructibilit´e des ´el´ements de K0=Qest une cons´equence
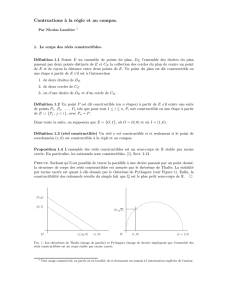
directe du th´eor`eme de Thal`es (voir Figure 1). Supposons maintenant que les ´el´ements de Kisont
constructibles pour un certain i≤n−1. Comme l’extension Ki+1 ⊂Kiest de degr´e 2, il suffit de
montrer que l’ensemble des r´eels constructibles est stable par racine carr´ee, ce qui est assur´e par
le th´eor`eme de Pythagore (voir Figure 1). Puisque L=Kn, le r´esultat s’ensuit. 

(x/y, 0) (x, 0)O
(0,1)
(0, y)
O(x+ 1,0)(1,0)
(0,√x)
Fig. 1. Les th´eor`emes de Thal`es (image de gauche) et Pythagore (image de droite) impliquent que l’ensemble des
r´eels constructibles est un corps stable par racine carr´ee.
R´ef´erences
[1] Jean-Claude Carrega. Th´eorie des corps. La r`egle et le compas. Hermann, 1989.
[2] Herv´e Francinou, Serge Gianella. Exercices de math´ematiques pour l’agr´egation, alg`ebre 1.
Masson, 1995.
[3] Xavier Gourdon. Les maths en tˆete. Alg`ebre. Ellipses, 1994.
[4] Daniel Perrin. Cours d’alg`ebre. Ellipses, 1996.