Dimension d`un espace vectoriel. Exemples et applications.

Dimension d’un espace vectoriel. Exemples et applications.
Par Nicolas Lanchier
1
1. Théorie de la dimension.
Dans toute la suite, K désigne un corps commutatif et E un K-espace vectoriel.
Définition 1.1 Une famille (xi )i∈I de vecteurs de E est dite libre si
X
λi xi = 0 =⇒ λi = 0 ∀ i ∈ I.
i∈I
Définition 1.2 Une partie A ⊂ E est dite génératrice si vect(A) = E. [3], Sect. 3.1
Définition 1.3 On appelle base du K-espace vectoriel E toute famille (xi )i∈I ⊂ E à la fois libre
et génératrice. [3], Sect. 3.1
Définition 1.4 On dira que E est de dimension finie, ce que l’on supposera systématiquement
par la suite, s’il existe une famille génératrice finie de E. [3], Sect. 3.1
Théorème 1.5 (base incomplète) Soient G un système fini de générateurs de E et L ⊂ G un
système libre. Alors il existe une base B de E telle que L ⊂ B ⊂ G. [3], Sect. 3.1
Théorème 1.6 Toutes les bases de E ont même cardinal n. L’entier n ainsi défini est appelé
dimension de E, ce que l’on notera dim E = n. [3], Sect. 3.1
Proposition 1.7 Soient E1 et E2 deux sous-espaces vectoriels de E. Alors les conditions suivantes
sont équivalentes :
1. E = E1 ⊕ E2 .
2. dim E = dim E1 + dim E2 et E1 ∩ E2 = {0}.
3. dim E = dim E1 + dim E2 et E = E1 + E2 . [3], Sect. 3.1
Théorème 1.8 (théorème du rang) Soient F un K-espace vectoriel et f : E −→ F une application linéaire. Alors f est de rang fini et dim E = dim Ker f + rg f . [3], Sect. 3.2
Théorème 1.9 Si F est un sous-espace vectoriel de E alors dim E = dim F + dim F ⊥ . De même,
si G est un sous-espace vectoriel de l’espace dual E ∗ alors dim E ∗ = dim G + dim G◦ . [3], Sect. 3.4
2. Application aux invariants de similitudes.
Définition 2.1 Soient E un K-espace vectoriel de dimension finie et f ∈ L(E) une application
linéaire. Pour tout x ∈ E, on appelle polynôme minimal de x relatif à f l’unique polynôme unitaire
de plus bas degré Px ∈ K[X] tel que Px (f )(x) = 0. [3], Sect. 4.2
Proposition 2.2 Ex = {P (f )(x) : P ∈ K[X]} est un espace vectoriel de dimension deg(Px ). [3],
Sect. 4.2
Définition 2.3 Une application linéaire f ∈ L(E) est dite cyclique s’il existe x ∈ E tel que
E = Ex . [3], Sect. B.1
1
Tout usage commercial, en partie ou en totalité, de ce document est soumis à l’autorisation explicite de l’auteur.
Théorème 2.4 Etant donné f ∈ L(E), il existe une suite F1 , F2 , · · · , Fr de sous-espaces vectoriels
de E stables par f et tels que
1. E = F1 ⊕ F2 ⊕ · · · ⊕ Fr .
2. Pour tout 1 ≤ i ≤ r, la restriction fi de f à Fi est un endomorphisme cyclique de Fi .
3. Si Pi désigne le polynôme minimal de fi alors pour tout 1 ≤ i ≤ r, Pi+1 divise Pi .
De plus, la suite P1 , P2 , · · · , Pr ne dépend que de f et non du choix de la décomposition. On
l’appelle suite des invariants de similitude de f . [3], Sect. B.1
Application 2.5 (réduction de Frobenius) Notons P1 , P2 , · · · , Pr la suite des invariants de
similitude de f ∈ L(E) et pour tout 1 ≤ i ≤ r, C(Pi ) la matrice compagnon de Pi . Alors il existe
une base de E dans laquelle la matrice de f est donnée par


A = 
C(P1 )
0
..
.
0
C(Pr )



[3], Sect. B.1
3. Extensions de corps et points constructibles.
Définition 3.1 Le degré d’une extension de corps K ⊂ L est égal à la dimension de L vu comme
espace vectoriel sur le corps K. Le degré de K ⊂ L est noté [L : K].
Théorème 3.2 (multiplicativité des degrés) Soient K ⊂ M une extension de corps et L un
corps intermédiaire entre K et M . Alors
[M : K] = [M : L] · [L : K].
Preuve. Étant données (a1 , a2 , . . . , an ) une base du K-espace vectoriel L et (b1 , b2 , . . . , bm ) une
base du L-espace vectoriel M , il est facile de voir que
(a1 b1 , a1 b2 , . . . , a1 bm , a2 b1 , . . . , an b1 , . . . , an bm )
est une base du K-espace vectoriel M . En notant que son cardinal est égal à n × m, la conclusion
est immédiate. Théorème 3.3 Soient K ⊂ L une extension de corps et a un élément de L. Alors a est algébrique
sur K si et seulement si dimK K(a) < ∞. [4], Sect. 3.1
Théorème 3.4 (Wantzel) Tout réel constructible est algébrique sur Q de degré une puissance
de 2. [1], Sect. 2.22
Preuve. Étant donné x un réel constructible, il existe une suite croissante A0 ⊂ · · · ⊂ An de
parties de R2 telles que
1. A0 = {O, I}.
2. Ai = Ai−1 ∪ {Pi } avec Pi constructible en une étape à partir de Ai−1 .
3. (x, 0) ∈ An .
Notons alors Ki le corps engendré par les coordonnées des points de Ai de sorte que K0 = Q
et x ∈ Kn . Les équations de droites ou de cercles étant de degré ≤ 2, il n’est pas difficile de
montrer que [Ki : Ki−1 ] ≤ 2. La formule de multiplicativité des degrés implique que
[Kn : Q ] = [Kn : Kn−1 ] · [Kn−1 : Kn−2 ] · · · [K1 : Q ] = 2m
= [Kn : Q(x)] · [Q(x) : Q ].
Il en résulte que x est algébrique et que [Q(x) : Q ] est une puissance de 2.
Corollaire 3.5 Il est impossible de dupliquer un cube à la règle et au compas.
√
Preuve. En tant que racine du polynôme irréductible
X 3 − 2, le réel 3 2 est algébrique sur Q de
√
degré 3. Il résulte du théorème de Wantzel que 3 2 n’est pas constructible à la règle et au compas
d’où bien sûr l’impossibilité de dupliquer un cube. Corollaire 3.6 Il est impossible de trisecter un angle à la règle et au compas.
Preuve. Montrons par exemple que l’angle π/3 ne peut pas être trisecté, i.e. que le réel a =
cos(π/9) n’est pas constructible. L’équation cos 3θ = 4 cos3 θ − 3 cos θ montre que a est racine
du polynôme irréductible 4X 3 − 3X − 1. En particulier, a est algébrique de degré 3 donc non
constructible en vertu du théorème de Wantzel. Lemme 3.7 Etant donné G un p-groupe d’ordre pn il existe une suite G0 ⊂ · · · ⊂ Gn de sousgroupes distingués de G tels que |Gi | = pi pour tout 0 ≤ i ≤ n. [2], Ex. 1.4
Théorème 3.8 Soient L un sous-corps de R et (x, y) un élément de L2 . Si l’extension Q ⊂ L est
normale de degré une puissance de 2 alors le point de coordonnées (x, y) est constructible à la
règle et au compas. [2], Ex 4.14
Preuve. Soit G = Gal(L | Q) le groupe de Galois de l’extension Q ⊂ L. Cette extension étant
normale, il résulte du théorème de correspondance de Galois que |G| = [L : Q ] = 2n . En particulier,
d’après le lemme 3.7, il existe une suite G0 ⊂ · · · ⊂ Gn de sous-groupes distingués de G tels que
|Gi | = 2i pour tout 0 ≤ i ≤ n. Notons Ki = inv(Gn−i ) le corps des invariants de Gn−i soit
Ki = {x ∈ L : σ(x) = x pour tout σ ∈ Gn−i }.
Il est clair que K0 = Q et Kn = L. Par ailleurs, comme (Gn−i : Gn−i−1 ) = 2, Gn−i−1 est également
distingué dans Gn−i . Une nouvelle application du théorème de correspondance nous permet alors
d’affirmer que
[Ki+1 : Ki ] = | Gal(Ki+1 | Ki )| = (Gn−i : Gn−i−1 ) = 2.
Pour conclure, montrons par récurrence que les éléments de Ki , 0 ≤ i ≤ n, sont constructibles à la
règle et au compas. Tout d’abord, la constructibilité des éléments de K0 = Q est une conséquence
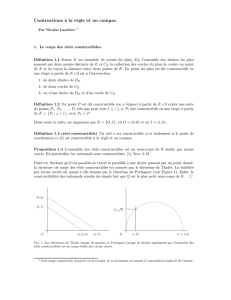
directe du théorème de Thalès (voir Figure 1). Supposons maintenant que les éléments de Ki sont
constructibles pour un certain i ≤ n − 1. Comme l’extension Ki+1 ⊂ Ki est de degré 2, il suffit de
montrer que l’ensemble des réels constructibles est stable par racine carrée, ce qui est assuré par
le théorème de Pythagore (voir Figure 1). Puisque L = Kn , le résultat s’ensuit. (0, y)
(0, 1)
O
(0,
(x/y, 0)
(x, 0)
√
x)
O
(1, 0)
(x + 1, 0)
Fig. 1. Les théorèmes de Thalès (image de gauche) et Pythagore (image de droite) impliquent que l’ensemble des
réels constructibles est un corps stable par racine carrée.
Références
[1] Jean-Claude Carrega. Théorie des corps. La règle et le compas. Hermann, 1989.
[2] Hervé Francinou, Serge Gianella. Exercices de mathématiques pour l’agrégation, algèbre 1.
Masson, 1995.
[3] Xavier Gourdon. Les maths en tête. Algèbre. Ellipses, 1994.
[4] Daniel Perrin. Cours d’algèbre. Ellipses, 1996.