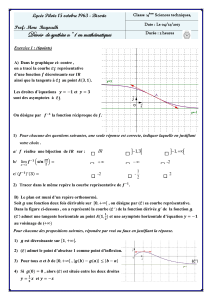
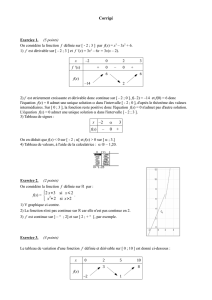
MSI 101

SECONDE EDITION
JUIN 2008
MSI 101
PROPOSITION DE COURS
Agnès Bachelot – Bernadette Munos

Table des matières
1 Bases de logique et théorie des ensembles 1
1.1 Opérations logiques - Raisonnements . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.2 Ensembles et parties d’un ensemble . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.2.1 Ensemblesetéléments................................. 1
1.2.2 Sous-ensembles..................................... 1
1.2.3 Produitd’ensembles .................................. 2
1.2.4 Rappel:quantificateurs ................................ 2
1.2.5 Opérations sur les ensembles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.3 Notiond’application ...................................... 3
1.3.1 Application d’un ensemble Edans un ensemble F; exemples . . . . . . . . . . . 3
1.3.2 Image directe, image réciproque . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.3.3 Composition des applications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.3.4 Famille d’éléments d’un ensemble . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.3.5 Injection, surjection, bijection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2 Nombres entiers - Dénombrement- Initiation à l’arithmétique - Nombres rationnels 7
2.1 Nombresentiers ........................................ 7
2.1.1 Relation d’ordre dans un ensemble . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.1.2 Lesentiers........................................ 7
2.1.3 Dénombrement..................................... 8
2.2 Arithmétique dans Z...................................... 9
2.3 Lesrationnels.......................................... 11
3 Nombres réels et propriétés de R13
3.1 Propriétés de R......................................... 13
3.1.1 Corps totalement ordonné . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
3.1.2 Rpossède la propriété de la borne supérieure . . . . . . . . . . . . . . . . . . . . 14
3.1.3 Valeurabsolue ..................................... 14
3.2 Intervalles de R......................................... 15
3.3 Propriétés des rationnels et irrationnels . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
4 Nombres complexes 17
4.1 Définitions............................................ 17
4.2 Propriétés............................................ 18
4.3 Formetrigonométrique..................................... 18
4.4 Exponentiellecomplexe .................................... 18
4.5 Résolution d’équations dans C................................ 19
4.5.1 Racines n-ièmes .................................... 19
i

ii TABLE DES MATIÈRES
4.5.2 Equationduseconddegré............................... 19
5 Suites réelles 21
5.1 Généralités ........................................... 21
5.2 Convergence d’une suite réelle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
5.3 Opérations sur les suites convergentes . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
5.4 Généralisation.......................................... 22
5.5 Théorèmes d’existence de limites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
5.6 Exemples ............................................ 24
6 Fonctions numériques 25
6.1 Généralitéssurlesfonctions.................................. 25
6.2 Limite.............................................. 25
6.2.1 Limite d’une fonction en un point de Rou de R∪ {−∞,+∞} ........... 25
6.2.2 Opérations sur les limites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
6.2.3 Théorèmes sur les limites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
6.3 Continuité............................................ 28
6.3.1 Définitions ....................................... 28
6.3.2 Propriétés........................................ 28
6.3.3 Fonctions continues sur un intervalle . . . . . . . . . . . . . . . . . . . . . . . . . 28
6.4 Dérivabilité ........................................... 29
6.4.1 Définitions ....................................... 29
6.4.2 Opérations sur les dérivées . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
6.4.3 Propriétés des fonctions dérivables . . . . . . . . . . . . . . . . . . . . . . . . . . 30
6.4.4 Dérivéessuccessives .................................. 31
7 Fonctions numériques usuelles 33
7.1 Fonctions logarithme et exponentielle (rappels) . . . . . . . . . . . . . . . . . . . . . . . 33
7.1.1 Logarithmenépérien.................................. 33
7.1.2 Exponentielle de base e................................ 34
7.1.3 Fonctionspuissances.................................. 34
7.1.4 Croissancescomparées................................. 34
7.2 Fonctions circulaires et leurs réciproques . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
7.2.1 Fonctionscirculaires .................................. 34
7.2.2 Fonctions circulaires réciproques . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
7.3 Fonctions hyperboliques et leurs réciproques . . . . . . . . . . . . . . . . . . . . . . . . . 36
7.3.1 Fonctionshyperboliques................................ 36
7.3.2 Fonctions hyperboliques réciproques . . . . . . . . . . . . . . . . . . . . . . . . . 36
8 Intégration, calcul de primitives 39
8.1 Introduction .......................................... 39
8.1.1 Définition rapide car pas au programme de ce semestre . . . . . . . . . . . . . . 39
8.1.2 Notationetformules.................................. 40
8.2 Primitive d’une fonction continue sur un intervalle ouvert de R.............. 41
8.3 Calculs d’intégrales et calculs de primitives . . . . . . . . . . . . . . . . . . . . . . . . . 42

TABLE DES MATIÈRES iii
9 Equations différentielles 43
9.1 Généralités sur les équations différentielles linéaires . . . . . . . . . . . . . . . . . . . . . 43
9.2 Equations différentielles linéaires d’ordre 1 . . . . . . . . . . . . . . . . . . . . . . . . . . 43
9.2.1 Généralités ....................................... 43
9.2.2 Résolution:....................................... 44
9.3 Equations différentielles linéaires d’ordre 2 à coefficients constants . . . . . . . . . . . . 44
9.3.1 Généralités ....................................... 44
9.3.2 Résolution de ay00 +by0+cy = 0 ........................... 44
9.3.3 Résolution de ay00 +by0+cy =f........................... 45
10 Fonctions de 2 ou 3 variables réelles 47
10.1Rappelsetcompléments.................................... 47
10.2 Dérivées partielles de fonctions de 2ou 3variables réelles . . . . . . . . . . . . . . . . . 48
10.2.1 Dérivées partielles premières . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
10.3 Gradient, divergence, rotationnel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
10.3.1 Vocabulaire....................................... 48
10.3.2 Gradient d’une fonction scalaire . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
10.3.3 Divergence et rotationnel d’un champ de vecteurs . . . . . . . . . . . . . . . . . . 49