Sixième - Chapitre 2 - Séance 03 - Académie d`Orléans

Activité 3 : Utiliser une division euclidienne J’ai déjà vu
Suite à un concours remporté par les élèves, le « club Sciences » a gagné un lot de 200 livres. Les neufs élèves
du club désirent se partager équitablement ce lot. Les livres restants iront au CDI.
Il faut donc former 9 piles contenant chacune le même nombre de livres.
1. Méthode de Luc : Luc met un livre dans chacune des neuf piles, puis un deuxième, etc.
Il continue jusqu’à ce qu’il n’y ait plus assez de livres pour remplir toutes les piles.
a. Calculer, à l’aide de soustractions successives, le nombre de livres qu’il restera à Luc après chaque
étape. Il faut retrancher mentalement 9 : 200, 191, 182…
200 - 9 = 191 ; 191 - 9 = 182 ; 182 - 9 = 173 ; 173 - 9 = 164 ; 164 - 9 = 155 ; 155 - 9 = 146 ;
146 - 9 = 137 ; 137 - 9 = 128 ; 128 - 9 = 119 ; 119 - 9 = 110 ; 110 - 9 = 101 ; 101 - 9 = 92 ;
92 - 9 = 83 ; 83 - 9 = 74 ; 74 - 9 = 65 ; 65 - 9 = 56 ; 56 - 9 = 47 ; 47 - 9 = 38 ;
38 - 9 = 29 ; 29 - 9 = 20 ; 20 - 9 = 11 ; 11 - 9 = 2.
Après la dernière étape, il lui restera 2 livres. Il y aura eu en tout 22 étapes.
b. En déduire le nombre de livres que Luc mettra dans chaque pile. Combien restera-t-il de livres ?
Luc mettra 22 livres dans chaque pile, il restera 2 livres.
2. Méthode de Julie : Julie a trouvé le nombre de livres qu’elle peut mettre dans chaque pile à l’aide d’une
seule opération étudiée à l’école primaire.
a. Déterminer de quelle opération il s’agit. Poser et effectuer cette opération.
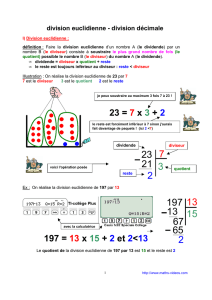
Il s’agit d’une division euclidienne : 2 0 0 │ 9
- 1 8 │ 2 2
2 0 │
- 1 8 │
2 │
b. Préciser le nombre de livres que recevra chaque élève, ainsi que le nombre de livres qui seront donnés
au CDI.
Chaque élève recevra 22 livres ; 2 livres seront donnés au CDI.
3. Quelle méthode est la plus rapide ? Celle de Julie !
─────────────────────────────────────────────────────────────
Définitions 4 : La division euclidienne d’un nombre entier (appelé dividende) par un nombre entier (appelé
diviseur) permet de trouver deux nombres, appelés quotient euclidien et reste, vérifiant les
conditions :
 dividende = (diviseur × quotient euclidien) + reste
 le reste est strictement inférieur au diviseur
Euclide fait ses études à l’Académie, école fondée par Platon à Athènes, où il apprend la
géométrie. Il participe également à la vie politique.
Il s’installe à Alexandrie sous l’invitation du pharaon. Il travaille au musée d’Alexandrie et
fonde une école qui devient très célèbre.
Il réunit dans un ouvrage de 13 volumes, Éléments, toutes les connaissances mathématiques de
son époque. On lui doit entre autres la division en nombres entiers qui porte son nom : la
division euclidienne.
Exemple : • Division euclidienne de 498 par 17 :
dividende diviseur
↪
↪↪
↪ 4 9 8 │ 1 7 ↩
↩↩
↩
- 3 4 │ 2 9
1 5 8 │ ⤤
⤤⤤
⤤ quotient
- 1 5 3 │
5 │
reste ⤣
⤣⤣
⤣
L’égalité correspondante est : 498 = (17 × 29) + 5

───────────────────────────────────────────────────────────────────
───────────────────────────────────────────────────────────────────
Méthode 2 : Résoudre un problème en effectuant une division euclidienne
1 On présente les calculs que l’on va effectuer par une phrase.
2 On effectue la division euclidienne.
3 On écrit l’égalité correspondante.
On interprète les résultats de la division euclidienne.
On conclut par une phrase.
Dans sa collection, Théo possède 344 timbres. Il souhaite les ranger dans son album qui peut
contenir 25 timbres par pages. De combien de pages aura-t-il besoin pour ranger tous ses timbres ?
Calculons le nombre de pages dont Théo aura besoin : 3 4 4 │ 2 5
- 2 5 │ 1 3
9 4 │
- 7 5 │
1 9 │
344 = (13 × 25) + 19
Il y aura 13 pages comportant 25 timbres et 1 page (la dernière) comportant 19 timbres.
Théo aura donc besoin de 14 pages.
Définitions 5 : Dans une division euclidienne, si le reste est 0, on dit que :
• le dividende est un multiple du diviseur ;
• le dividende est divisible par le diviseur.
Exemple : • 105 = (7 × 15) + 0
105 = 7 × 15
105 est donc un multiple de 7 : 105 est divisible par 7.
───────────────────────────────────────────────────────────────────
Exercice 5 : Sans poser l’opération
On a 165 = 20 × 8 + 5.
1. Donner le quotient entier et le reste de la division
euclidienne de 165 par 8.
2. Donner le quotient entier et le reste de la division
euclidienne de 165 par 20.
Exercice 6 : Sans poser l’opération
On a 135 = 7 × 18 + 9.
1. Donner le quotient entier et le reste de la division
euclidienne de 135 par 18.
2. Donner le quotient entier et le reste de la division
euclidienne de 135 par 7.
Exercice 7 :
Recopier puis compléter les divisions euclidiennes.
a.
5 5 7 3 b. 3 8 0 7
-
•
•
• • - • •
•
•
•
•
•
•
-
• •
- •
•
•
•
•
- •
•
•
c.
8 1 6 6 d. 8 2 7 4
•
•
•
• • • •
•
• •
•
•
•
•
• •
Exercice 8 :
Julien veut ranger un paquet de 100 feuilles dans son classeur.
Le professeur a demandé 6 parties dans le classeur et Julien
veut placer le même nombre de feuilles dans chaque partie.
1. Combien place-t-il de feuilles dans chaque partie ?
2. Combien lui restera-t-il de feuilles ?
Exercice 9 :
Le principal d’un collège a convoqué les 232 élèves de 6
ème
dans
la grande salle d’étude. Les surveillants ont disposé les sièges par
rangées de 18.
1. Combien faut-il prévoir de rangées ?
2. Combien reste-t-il de places libres dans la dernière rangée ?

Exercice 10 :
Un agriculteur doit ranger 400 pommes dans des cagettes. Une
cagette peut contenir 24 pommes.
1. Combien doit-il utiliser de cagettes pour ranger toutes les
pommes ?
2. Combien lui manque-t-il de pommes pour remplir la
dernière cagette ?
Exercice 11 :
Le directeur doit acheter des balles pour le nouveau club de ping-
pong. À l’entraînement, il faut quatre balles par joueur. Les
balles sont vendues par lots de 8. Il y a 15 élèves inscrits.
Combien de lots doit-il acheter ?