Continuiteserie1 (1)

1
1°) Soit
( ) 3 6f x x
.
a) Peut-on parler de la continuité de f en 1 et
en 2 ?
b) Montrer que pour tous réels a et b, on a
a b a b  
c) Montrer que
( ) (1) 3 1f x f x  
.
d) Montrer alors que f est continue en 1.
e) Montrer de même que f est continue en 2.
2°) Soit
( ) 2 5g x x
.
a) Peut-on parler de la continuité de g en –2 et en
–3 ?
b) Montrer que
24
2 5 1 2 5 1
x
xx
.
c) En déduire que
2 5 1 2 2xx   
.
d) Montrer alors que g est continue en –2.
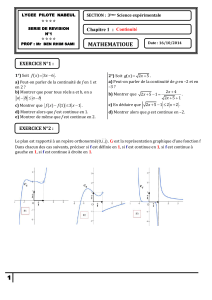
Le plan est rapporté à un repère orthonormé
(O,i,j)
. Cf est la représentation graphique d’une fonction f
Dans chacun des cas suivants, préciser si f est définie en 1, si f est continue en 1, si f est continue à
gauche en 1, si f est continue à droite en 1.
EXERCICE N°2 :
LYCEE PILOTE NABEUL
✫✫✫✫
SERIE DE REVISION
N°1
✫✫✫✫
PROF : Mr BEN RHIM SAMI
SECTION : 3ème Science expérimentale
Chapitre 1 : Continuité
MATHEMATIQUE
Date : 16/10/2014
EXERCICE N°1 :

2
Soit la fonction définie par
10
2 4 0 3
13
f x x si x
f x x si x
f x x si x
1°) Tracer la courbe représentative de f dans
un repère
( , , )O i j
2°) a) Justifier que la fonction f est continue sur
,0
b) Justifier que la fonction f est continue sur
0, 3
c) Justifier que la fonction f est continue sur
3, 
3°) Justifier à l’aide du graphique, que la fonction
f n’est pas continue sur IR.
2
si 0
Soit : si 0 1
1 si 1
xx
f x x x
xx
On désigne par c la courbe représentative de f dans un repère orthonormé
( , , )O i j
EXERCICE N°3 :
EXERCICE N°4 :

3
1°) Tracer c.
2°)
f
est-elle continue en 0 ?
3°)
f
est-elle continue à gauche en 1 ?
4°)
f
est-elle continue à droite en 1 ?
5°) Sur quelle partie de IR,
f
est-elle continue ?
6°) Dresser le tableau de variation de
f
.
7°) Déterminer, l'image par
f
de chacun des
intervalles :
1
,0 ; 0, ; 1,
2
Dans le plan muni d’un un repère
( , , )O i j
, on a représenté
la fonction f définie par :
33f x x x
1°) Justifier, graphiquement, que l’équation
3fx
admet
une solution unique
0
x
dans IR et en donner un
encadrement à
3
10
près.
2°) Déterminer les abscisses des points d’intersection de (C)
et la droite
': 2y
On considère la fonction f définie par :
1,1
2 2 1,
si x
x
x si
I- 1°) Déterminer l’ensemble de définition de f.
2°) Tracer la courbe représentative de f dans un repère
( , , )O i j
.
3°) a) Justifier le continuité de la fonction f sur
;1 
et sur
1; 
.
b) Vérifier, à l’aide du graphique, que la fonction f n’est pas continue sur IR.
4°) Pour chacune des équations suivantes, déterminer, à l’aide du graphique, le nombre de solutions
de l’équation :
( ) 0fx
;
( ) 0fx
et
( ) 2fx
.
II- 1°) Quelles sont les images par f des intervalles :
3; 2I  
,
2;1J
et
1;K  
.
2°) Déterminer l’ensemble des antécédents par f des réels de l’intervalle
1,1
2
.
Soit la fonction
²2
:2
x x x
fx x
1°) a) Déterminer l’ensemble de définition
f
D
de
f.
b) Montrer que pour tout x
f
D
;
2
( ) 1
2
x
fx x
2°) Montrer que f est continue sur son ensemble
de définition
f
D
3°) a) Étudier les variations de f sur
f
D
.
b) Montrer que f est bornée sur
4; 2
4°) a) Calculer f(2) et f(3).
b) En déduire que l’équation f(x) = 0 admet
dans [2, 3] une solution puis déterminer une
valeur approchée de à
1
10
près.
EXERCICE N°5 :
EXERCICE N°6 :
EXERCICE N°7 :

4
I- Soit f la fonction définie sur IR par :
3
( ) 2 1f x x x   
.
1°) Montrer que f est strictement décroissante sur IR.
2°) Quelles sont les images par f des intervalles :
1;3
;
2;5J
; et
1;1K
.
3°) a) Montrer que l’équation :
( ) 0fx
admet une solution dans l’intervalle
0;1
.
b) Donner une valeur approchée par défaut à 0,1 prés de .
II- Soit g la fonction définie sur IR par :
2
( ) 5g x x x  
.
1°) Déterminer l’ensemble de définition de g.
2°) Etudier la continuité de g sur son ensemble de définition.
3°) a) Montrer que l’équation :
( ) 0gx 
admet une solution dans l’intervalle
1;2
b) Donner une valeur approchée par défaut à 0,1 prés de .
III- On considére la fonction h définie par :
( ) ; 4
() ( ) 4;
f x si x
hx g x si x
1°) Déterminer l’ensemble de définition de h.
2°) Etudier la continuité de h sur son ensemble de définition.
1°) f est une fonction impaire définie sur  par :
a) Compléter le traçage de Cf.
b) Etudier graphiquement la continuité de f en 0.
c) Donner un majorant et un minorant de f.
2°) On donne une fonction g paire définie par :
   .
a) Déterminer l’ensemble de définition de g noté Dg et tracer Cg sur le même repère avec une autre
couleur.
b) Etudier graphiquement les variations de g.
c) Donner l’expression de g(x) si   .
d) Utiliser Cg pour déterminer g([1,2]) et g(]1,3])
e) Montrer que l’équation g(x)=0 admet une seule solution  dans  et donner un encadrement
de cette solution à 10–1 prés.
3°) On considère la fonction h définie sur IR par   .
a) Pour quelle valeur de x la fonction h présente un maximum ? quelle est la valeur de cette
maximum ?
b) Tracer la représentation graphique de h sur le même repère.
c) Donner un encadrement d’amplitude 1 de la solution  de l’équation h(x)=g(x).
4°) Soit la fonction   .
a) Etudier la continuité de la fonction k sur [0,1].
b) Donner un encadrement de  à 10-1 prés.
EXERCICE N°8 :
EXERCICE N°9 :