01 fonctions coursimp

Généralités sur les fonctions numériques
1. Rappels sur les fonctions
1.1. Généralités
 fx
fxxffx fx
  x  
Df
yfxDf fx y
!"x#fx
f
!$
$%
&  '    (    
)   
*  +            $
 f 
f
, 
"fDf 
 -.Df 
f. x∈.x∈.
x/xf (x)f (x')
f. x∈.
x∈.x/xf (x)/f (x)
0%
f .  x∈. x∈.
x/xf (x)f (x')
f. x∈.
x∈.x/xf (x)>f (x')
0%
 -fDf 
+
f−x= fx
x∈Df
−x∈Df
+
f−x=− fx
x∈Df
−x∈Df
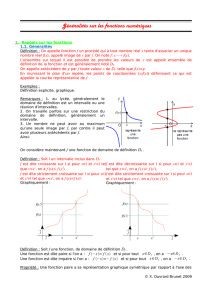
1 +%($
234)556
x
f(x)
f(x')
x'
i
j
x'
f(x')
f(x)
x
i
j

+            %  (          
"
1.2. Fonctions de référence.
1.2.1. Fonctions affines.
71  -$$ $8
ℝ
%
( $8
$
1 
-95
- 5
-/5
: 
-$$$$$
x≠x'
$
fx '−fx
x '−x
$$
234)556
x
f(-x) = f(x)
i
j
-x
x
f(x)
i
j
f(-x) = -f(x)
-x

-$$ $8$
&$
:7$ 
"
x');
fx5')
f<
&%%
.=$
1.2.2. La fonction carré.
71   x  x>  
ℝ
ℝ7
ℝ8
%
1 :7x> x>x x>$
$(
,($> 
1 
x²=a
)' 5
/5 
0%$   $>
( 
1.2.3. La fonction inverse.
       x 
'
x
ℝ?
]−∞ ;5[
]5;∞[
%%(
1  : 
'
−x=−' x
 x 
'
x
"(%(
234)556

1.2.4. La fonction racine carrée
 x 
x
ℝ8
]5;∞[
         %      7  
5
&   
x
x5
x5
x
)=x
1.2.5. La fonction valeur absolue
 x @x@
ℝ
x/5|x| 7xx5|x| x!
ℝ7
ℝ8
1.2.6. Les fonctions trigonométriques
 x xx x)
%A
234)556

2. Opérations sur les fonctions
2.1. Égalité de deux fonctions
  $ f  g  Df   Dg  
Df  Dg x∈Df fx gx
!$  fx
x²)x*
x−)
gx
x;''
x−)
B
ℝ∖ { ) }
 fx gx  x 
2.2. Somme et différence de fonctions
!$' 
"fx 
'
x
gx x>8*
x fx8gxx fx7gx
5C!$$
'Cfg
)CD
*CEF
 -$fDfDg
f8gxDf ∩ Dg
f8gx fx8gx
f7gxDf ∩ Dg
f7gx fx7gx
!$ 
fx= x)
gx= *−x
[−)G ;∞[
]−∞;*]
8H7)#*I
fgx= x−) *−x
7H7)#*I
f−gx= x−)− *−x
1 8
(B
7
((B
1 -B.8
B.
-.7B
.
:7$ 
1$(
B
$ $>8
x
$ 7$>
234)556
x x x  x