Sens de variation de la fonction affine f(x) = ax + b. Si a > 0 alors f

Sens de variation de la fonction affine f(x) = ax + b.
Si a > 0 alors f est strictement croissante sur IR.
Si a < 0 alors f est strictement décroissante sur IR.
Si a = 0 alors f est constante sur IR. La représentation graphique est alors une droite parallèle à
l’axe des abscisses.
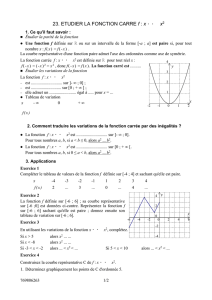
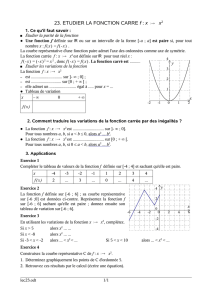
B. Fonction carré.
f(x) = x². Son ensemble de définition est Df = IR.
Tableau de variation :
x
– 0 +
f(x)
0
Sa courbe, représentée ci-dessous s’appelle parabole. Elle est symétrique par rapport à l’axe
des ordonnées.
C. Fonction inverse
f(x) = 1
x Son ensemble de définition est Df = IR \ {0} que l’on note aussi IR*. (L’étoile
signifie : privé de 0).
Tableau de variation :
x
– 0 +
f(x)
Sa courbe, représentée ci-dessous s’appelle hyperbole. Elle est symétrique par rapport à
origine du repère O.
2 3 4-1-2-3-4-5-6
2
3
4
5
6
7
8
9
-1
0 1
1
x
y
2 3 4 5-1-2-3-4-5
2
3
4
5
-1
-2
-3
-4
-5
0 1
1
x
y

II. Fonctions associées
Dans la suite, u est une fonction définie dans l’intervalle [a ;b].
A. f(x) = u(x + k) avec k  IR.
Exemple : u(x) = x² + 2 et k = 3
On a donc f(x) =
Tableaux de valeurs :
x
–3
–2
–1
0
1
2
3
x
–6
–5
–4
–3
–2
–1
0
u(x)
11
6
3
2
3
6
11
f(x)
11
6
3
2
3
6
11
Courbes :
Propriété : f(x) = u(x + k)
La courbe représentative de f est l’image de la courbe représentative de u par la translation de
vecteur
Conséquence : u est définie sur [a ;b]. f(x) = u(x + k).
B. f(x) = u(x) + k avec k  IR
Exemple : u(x) = 1
x et k = 2
On a donc f(x) =
2 3-1-2-3-4-5-6
2
3
4
5
6
7
8
9
10
11
-1
0 1
1
x
y

Tableaux de valeurs :
x
0,25
0,5
1
2
3
4
x
0,25
0,5
1
2
3
4
u(x)
4
2
1
0,5
0,33
0,25
f(x)
6
4
3
2,5
2,33
2,25
Courbes :
Propriété : f(x) = u(x) + k
La courbe représentative de f est l’image de la courbe représentative de u par la translation de
vecteur
Conséquence : u est définie sur [a ;b]. f(x) = u(x)+ k.
2 3 4
2
3
4
5
6
0 1
1
x
y