Modelisation des mecanismes

Spé
ATS COURS
Lycée P. Mendès France Epinal
Modélisation des Mécanismes - Etudiant.docx 1/38
MODELISATION
DES
MECANISMES

Spé
ATS COURS
Lycée P. Mendès France Epinal
Modélisation des Mécanismes - Etudiant.docx 2/38
SOMMAIRE
MODELISATION DES MECANISMES ................................................................................................................................................................... 4
Introduction : ................................................................................................................................................................ 4
1. Modélisation d'un mécanisme existant : .............................................................................................................. 4
a. Modélisation des pièces mécaniques : .................................................................................................. 5
b. Classes d'équivalences : ......................................................................................................................... 5
c. Modélisation des contacts : ................................................................................................................... 7
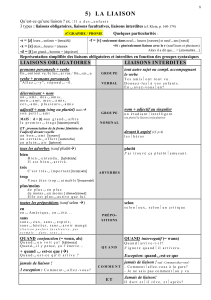
2. Etude des liaisons : ............................................................................................................................................... 7
a. Liaisons simples ou élémentaires .......................................................................................................... 7
b. Liaisons composées : ............................................................................................................................. 8
c. Torseur cinématique : ............................................................................................................................ 8
d. Torseur transmissible par une liaison parfaite : .................................................................................... 9
e. Liaison parfaite : .................................................................................................................................... 9
3. Torseurs associés aux liaisons classiques : .......................................................................................................... 11
a. Réciprocité du torseur d'action mécanique transmissible et du torseur cinématique : ..................... 12
b. Forme particulière des torseurs cinématiques : .................................................................................. 14
4. Liaisons obtenues par l'ajout de composants : ................................................................................................... 16
a. Les coussinets : .................................................................................................................................... 16
b. Les roulements à billes, à rouleaux ou à aiguilles : .............................................................................. 16
c. Les butées à billes et à rouleaux : ........................................................................................................ 16
d. Les douilles à billes ou à rouleaux : ..................................................................................................... 16
e. Les vis à billes : ..................................................................................................................................... 16
f. Les guidages à billes ou à rouleaux sur rails : ...................................................................................... 17
g. Les rotules lisses : ................................................................................................................................ 17
5. Représentations schématiques complémentaires : ............................................................................................ 17
a. Transmission par adhérence : roues à friction. ................................................................................... 17
b. Transmission par obstacles : Engrenages. ........................................................................................... 17
c. Transmission par obstacles : Pignon crémaillère. ................................................................................ 18
d. Transmission par obstacles : Roue et vis sans fin. ............................................................................... 18
e. Transmissions par lien flexible : pignons-chaîne. ................................................................................ 18
f. Transmissions par lien flexible : poulies-courroie. .............................................................................. 19
6. Schématisation : ................................................................................................................................................ 19
a. Graphe des contacts, des liaisons : ...................................................................................................... 19
b. Graphe de structure ou graphe des liaisons élémentaires : ................................................................ 21
c. Schéma cinématique minimal : ........................................................................................................... 21
d. Méthode pour représenter un schéma cinématique : ........................................................................ 22
7. Relation fondamentale de la théorie des mécanismes : ...................................................................................... 23
a. Mobilité (Principe de Maxwell et Kelvin) : ........................................................................................... 23
b. Relation fondamentale de la théorie des mécanismes : ..................................................................... 23
c. Système hyperstatique : ...................................................................................................................... 26
d. Application à la clé étau : ..................................................................................................................... 27

Spé
ATS COURS
Lycée P. Mendès France Epinal
Modélisation des Mécanismes - Etudiant.docx 3/38
8. Chaînes de solides - Structure des mécanismes : ................................................................................................ 27
a. Chaînes ouvertes : ............................................................................................................................... 28
b. Chaîne fermée simple : ........................................................................................................................ 29
c. Chaîne cinématiques complexes : ....................................................................................................... 30
9. Liaisons cinématiquement équivalentes : ........................................................................................................... 31
a. Liaisons en parallèle : .......................................................................................................................... 31
b. Liaison en série : .................................................................................................................................. 35

Spé
ATS COURS
Lycée P. Mendès France Epinal
Modélisation des Mécanismes - Etudiant.docx 4/38
MODELISATION DES MECANISMES
Problématique :
Comment obtenir un modèle du mécanisme représenté sous forme de schéma (image symbolique
simplifiée) permettant différentes études :
 Cinématique : - relations entrées-sorties en position et vitesse
- étude des mouvements
 Statique : - relations entrées-sorties en efforts
- efforts de liaisons entre solides
- efforts dans les liaisons
 Combinés : - Dynamique
- Energétique
Exemple : Nacelle élévatrice
INTRODUCTION :
Nous limiterons notre étude aux ensembles mécaniques constitués d’éléments rigides (solides) qui sont
en contact entre eux (assemblages).
Afin de permettre une bonne approche du mécanisme réel, on associe les pièces mécaniques à des
solides indéformables et, les liens entre elles, à des modèles de liaisons technologiques.
Mécanisme : - Un mécanisme est un agencement de pièces mécaniques reliées entre elles et conçu en vue de
réaliser une fonction déterminée.
- Un mécanisme est généralement conçu pour établir une relation particulière entre des
informations d’entrée qui sont des informations exercées par le milieu extérieur sur le
mécanisme, et des informations de sortie qui sont des informations exercées par le système sur
le milieu extérieur.
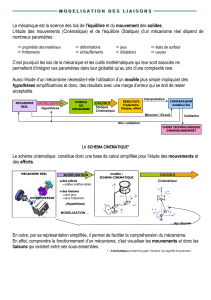
1. MODELISATION D'UN MECANISME EXISTANT :
Un mécanisme réel étant toujours très complexe, il est nécessaire, pour le comprendre et l’améliorer,
d’élaborer des modèles, afin de pouvoir lui appliquer les lois de la mathématique ou de la mécanique.
Cette modélisation permet de comprendre de façon fine le fonctionnement réel, d’en voir les limites et
de proposer des modifications sur le modèle afin de l’améliorer.

Spé
ATS COURS
Lycée P. Mendès France Epinal
Modélisation des Mécanismes - Etudiant.docx 5/38
Lors de l'étude d'un mécanisme, la modélisation des pièces, des liaisons et des actions mécaniques va
permettre de déterminer les performances de ce mécanisme et son dimensionnement. La modélisation et la
schématisation cinématiques sont des moyens privilégiés pour expliquer le fonctionnement d’un mécanisme et
pour exprimer certaines caractéristiques grâce à un paramétrage adéquat.
a. Modélisation des pièces mécaniques :
Solides parfaits, indéformables ayant une géométrie bien définie.
Cette modélisation exclut naturellement les fluides, ainsi que les pièces qui subissent de grandes
déformations, comme les ressorts ou les courroies de transmission.
b. Classes d'équivalences :
Un mécanisme est un agencement de pièces mécaniques reliées entre elles par des liaisons. Ces pièces
liées entre elles par des assemblages permettent :
- une transmission d’effort avec mouvement c’est le cas des systèmes de transformation de mouvement
(système bielle manivelle, réducteur, came….)
- une transmission d’effort sans mouvement c’est le cas de mécanisme de positionnement (montages
d’usinage…)
Afin de simplifier la représentation du mécanisme et la schématisation qui en résulte, il faut commencer
par regrouper tous les éléments en contact n'ayant aucun mouvement relatif pendant l'usage du mécanisme à
l'exception des pièces déformables. Chaque groupe constitue une classe d'équivalence selon la relation "pas de
mouvement relatif" et sera affecté d'un même repère (celui de la pièce la plus représentative du groupe de par
sa forme ou sa fonction).
L'intitulé "groupe cinématiquement lié" pourra également être utilisé pour définir ces groupes.
En principe on commence par repérer tous les éléments qui sont liés au bâti et qui serviront de référence
pour l’étude du mécanisme.
Application à la clé étau :
La clé étau est un outil très polyvalent. Légère et facile à manier, elle est très appréciée des différents
corps de métiers (mécanicien, carrossier, …). On la caractérise par sa capacité maximale d’ouverture des
mors : 23 mm.
Cet outillage peut intervenir sur de la boulonnerie détériorée ou mal
calibrée grâce à une force de serrage de 6000 N, mais peut servir
également pour maintenir en pression afin de coller, riveter,
souder… Dotée de mors doux (lisse), la clé peut être utilisée
sur une boulonnerie fragile, par exemple en plastique.
Modélisation
Modèle
amélioré
Mécanisme
réel amélioré
Mécanisme
réel
Concepts
simplificateurs
Etude critique du
modèle
Modifications des
dispositions
constructives