Cinématique du solide

Cinématique du solide page 1 / 4
Cinématique du solide.doc
Cinématique du s olide
1. Introduction.
Problématique : Existe-t-il un ‘objet’ mathématique qui permette de décrire la « vitesse » d’un solide par
rapport à un autre ?
Cet outil décrirait la manière dont se déplace le solide : c’est bien la définition empirique de la vitesse.
Outils mathématiques à notre disposition : le vecteur ne peut que représenter les vitesses des points.
Seul, il ne peut pas représenter la « vitesse » d’un solide.
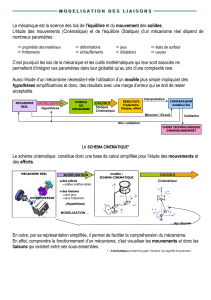
Solutions : un outil qui décrirait les vitesses de tous les points de ce solide, décrirait la vitesse du solide
lui même. Écrire la vitesse de tous les points, c’est écrire le champs des vitesses du solides.
2. Le champs des vitesses.
2.1 Torseur cinématique.
Soit deux points A et B fixes dans le solide 2. Une façon d’écrire que le solide est indéformable, c’est de
dire que le vecteur → AB ne varie pas dans le solide 2 (puisque ces deux points sont fixes dans 2).
d→ AB
dt 2 = →
0
En appliquant la relation de Boor, on montre facilement que :
→
vA,2/1 = → vB,2/1 + → AB ^ → Ω2/1
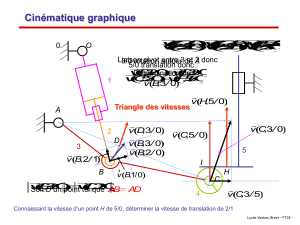
Il est possible de déterminer la vitesse de tous les points du solide, si on connaît, la vitesse d’un des
points, et le vecteur rotation.
Si on peut connaitre la vitesse de tous les points, on connaît la « vitesse » du solide.
→
vA,2/1 et → Ω2/1 sont donc nécessaires et suffisants pour exprimer la vitesse du solide 2 par rapport à 1.
• On crée ainsi un nouvel objet mathématique : le torseur cinématique
{V2/1} =
A
→
Ω2/1
→
vA, 2/1
=
B
→
Ω2/1
→
vB, 2/1
= …
avec → vA,2/1 = → vB,2/1 + → AB^→
Ω2/1
Remarques :
Le torseur sert aussi à exprimer d’autres grandeurs physiques (tout comme le vecteur).
Celui-ci est donc appelé torseur cinématique de 2 par rapport à 1 (d’où la notation).
→
Ω2/1 et → vA,2/1 sont les éléments de réduction du torseur.
A, B etc… sont les points de réduction du torseur

Cinématique du solide page 2 / 4
Cinématique du solide.doc
2.2 Torseurs cinématiques {V2/1} associés aux liaisons.
• Pivot d’axe (A, → x) entre le solide 2 et le solide 1.
→
Ω2/1 = ω.→ x
→
vA,2/1 = → 0
• Glissière de direction → x entre 2 et 1.
→
Ω2/1 = → 0
→
vM,2/1 = v.→ x
• Rotule de centre O.
→
Ω2/1 = quelconque
→
v0,2/1 = → 0
• Ponctuelle de centre O et de normale → n .
→
Ω2/1 = quelconque
→
v0,2/1.→ n= 0
• Pivot glissant d’axe (A, → x ).
→
Ω2/1 = ω.→ x
→
vA,2/1 = v.→ x
• Hélicoïdale d’axe (A, → x) de pas p.
→
Ω2/1 = ω.→ x & → vA,2/1 = v.→ x
avec v = p.ω
2.π
• Roulement sans glissement entre 2 et 1 quelles que soient les formes des solides.
(Roues de friction, boule qui roule, engrenage sur le diamètre primitif)
→
vA,2/1 = → 0
avec A le point de contact entre les pièces 2 et 1 (A est un point fixe pour aucune des deux pièces)
A
A
→
x
A
A
→
x
O
→
x
A
→
x
O
→
n
O

Cinématique du solide page 3 / 4
Cinématique du solide.doc
3. Composition des mouvements.
3.1 Définition.
• On pourrait montrer en utilisant la relation de Boor :
→
Ωn/1 = → Ωn/n-1 + … + → Ω3/2 + → Ω2/1 et → vM,n/1 = → vM,n/n-1 + … + → vM,3/2 + → vM,2/1
Même si M n’est pas fixe dans 1, 2 … n.
• Ce qui revient à dire : {Vn/1} = {Vn/n-1} + … + {V 3/2} + {V2/1} et {V2/1} = -{V1/2}
En pratique, on écrit la composition des vitesses en un point :
→
vA,n/1 = → vA,n/n-1 + … + → vA,3/2 + → vA,2/1
3.2 Fermeture cinématique.
(c’est la grande sœur de la relation de fermeture géométrique)
Si la chaîne cinématique forme une boucle fermée passant par les solides {1, 2, 3, …, n+1} avec 1 ≡ n+1
{V1/n} + … + {V 3/2} + {V2/1} = {0}
En pratique, écrire la fermeture cinématique en un point :
→
vA,1/n + → vA,n/n-1 + … + → vA,3/2 + → vA,2/1 = → 0
4. Utilisation.
♦ Pour déterminer la vitesse de n'importe quel point, en mécanique du solide, on utilise, dans l'ordre, les
deux types de relations suivantes :
• Compositions des vitesses :
Elle permet d’obtenir le vitesse d'un point en faisant apparaître les vitesses relatives aux différentes
liaisons de la chaîne cinématique.
• Champs des vitesses :
Connaissant chacune des liaisons et leurs caractéristiques cinématique, il est possible d’obtenir les
vitesses relatives à ces liaisons pour tous les points.
♦ Cette méthode donne les mêmes résultats que la méthode de dérivation : → vA,2/1 =
d→ O1A
dt 1
♦ Elle permet, en plus, de déterminer la vitesse d’un point qui n’appartient à aucun solide, contrairement
à la méthode de dérivation (cas du roulement sans glissement).

Cinématique du solide page 4 / 4
Cinématique du solide.doc
5. Applications aux liaisons équivalentes.
• liaison équivalente en série.
On montre que la liaison équivalente entre 3 et 1 est une liaison
linéaire annulaire de centre A et de direction → x .
Démonstration :
La composition des vitesse donne : → vA,3/1 = → vA,3/2 + → vA,2/1
→
Ω3/1 = → Ω3/2 + → Ω2/1
Champs de torseur : = v.→ x + → 0→ Ω3/1 = ω.→ x + quelconque
Conclusion : → vA,3/1 = v.→ x→ Ω3/1 = quelconque
• liaison équivalente de deux liaisons en parallèle.
Soit deux solides 1 et 2 liés par deux liaisons :
On montre que la liaison équivalente entre 1 et 2 est une liaison pivot d’axe (A, → x ).
Démonstration :
La fermeture cinématique s'écrit :
→
vA,2/1 rotule = → vA,2/1 pivo glissant
→
Ω2/1 rotule = → Ω2/1 pivot
Champs de torseur : → 0 = v.→ x quelconque = ω.→ x
Conclusion : → vA,2/1 = → 0→ Ω2/1 = ω.→ x
1
2
Rotule de centre A
Pivot glissant
d’axe (A, → x )
A
→
x
A
→
x
1
2
Pivot d’axe (A, → x )
1
2
3
Rotule de centre A
Pivot glissant
d’axe (A, → x )
A
→
x
A
→
x
1
3
linéaire annulaire de centre A et de direction → x