
Département de physique
PHYSIQUE DES VIBRATIONS
Jaouad DIYADI
2014
Introduction
On traitera dans ce cours 2 parties :
Vibrations : vibrations d’un oscillateur et couplages entre oscillateurs.
Ondes : propagation des vibrations.
Vibrations :oscillations périodiques d’un système (oscillateur), autour d’un point d’équilibre
stable. La plupart des systèmes physiques (système mécanique, électrique, thermodynamique
. . . etc). Ces oscillations ont lieu si le système est écarté de son point d’équilibre et des forces de
rappel tendent à le ramener vers ce point.
Ondes :évolutions spatiales et temporelles d’un système lorsque ses constituants peuvent ef-
fectuer des oscillations et interagir (transfert d’énergie) entre voisins sans transport de matière.
Les oscillations peuvent être de nature intrinsèque :
3ressort
3fil de torsion
ou d’un mouvement autour d’un équilibre stable :
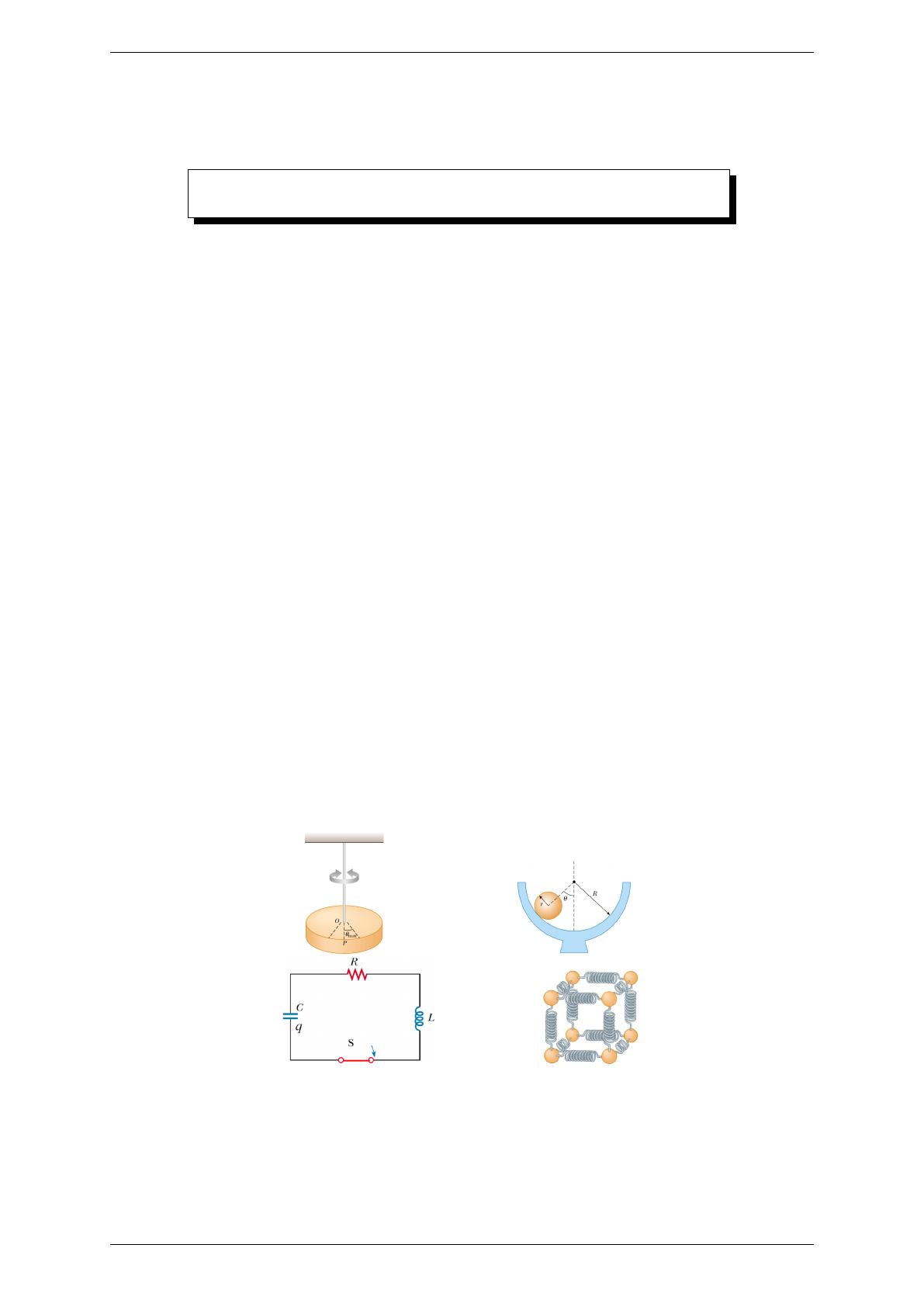
3une bille dans un bol
3modèle d’une liaison moléculaire
L’outil mathématique utilisé est l’équation différentielle linéaire d’ordre 2 à coefficients
constants
a2¨
x+a1˙
x+a0x=0
Parmi les phénomènes qui obéissent à cette équation on peut citer (en plus des oscillations
habituelles, masse attachée à un ressort ou un pendule, disque relié à un fil de torsion) les
oscillations de :
3charge électrique dans un circuit RLC
3charge électrique dans une antenne
3atome soumis à une excitation lumineuse
3interaction dans les réactions chimiques
3poutre en flexion
3croissance d’une colonie de bactérie en interaction avec la nourriture et le poison(que les
bactéries produisent)
3la population dans une forêt . . . etc
FIGURE 1 – Divers oscillateurs
Physique des vibrations 1Université Ibn Tofail

Table des matières
I Vibrations 5
1 Oscillations libres 6
1.1 Définitions......................................... 6
1.2 Oscillationslibres..................................... 6
1.2.1 Oscillateur harmonique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.2.2 LoideHookes................................... 7
1.2.3 Association de ressorts en série et en paralléle . . . . . . . . . . . . . . . . 7
1.2.4 EquationdeNewton............................... 8
1.2.5 Diagrammedephase............................... 8
1.3 Aspecténergétique .................................... 9
1.3.1 Biland’énergie .................................. 10
1.3.2 Valeurs moyennes des énergies potentielles et cinétiques . . . . . . . . . . 11
1.4 Autres types d’oscillateurs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1.4.1 Oscillateur électrique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
1.4.2 Pendulesimple.................................. 12
1.4.3 Oscillateurspatial ................................ 13
2 L’oscillateur amorti 15
2.1 Équationdumouvement................................. 15
2.1.1 Analogie avec le circuit électrique . . . . . . . . . . . . . . . . . . . . . . . 15
2.2 Solutions de l’équation du
mouvement ........................................ 17
2.2.1 Équation caractéristique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
2.2.2 Régime pseudo-périodique . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
2.2.3 Régimeapériodique ............................... 19
2.2.4 Régimecritique.................................. 19
2.3 Aspecténergétique .................................... 20
3 Oscillations forcées 21
3.1 Situationduproblème .................................. 21
3.2 Cas d’une excitation sinusoïdale . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
3.2.1 Étudedelasolution ............................... 22
3.2.2 Détermination de la solution forcée . . . . . . . . . . . . . . . . . . . . . . 22
3.3 Étude de l’amplitude en fonction
delafréquence ...................................... 25
3.3.1 ÉtudedelaRésonance.............................. 25
3.3.2 Bandespassantes................................. 26
4 Oscillations couplés 28
4.1 Oscillations libres d’un système
àdeuxdegrésdeliberté ................................. 28
4.1.1 Cas du couplage faible . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
4.1.2 Pulsations et modes propres . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
2

TABLE DES MATIÈRES TABLE DES MATIÈRES
4.1.3 Analogie électromécanique . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
4.2 Oscillations forcées d’oscillateurs
couplés........................................... 33
4.2.1 Système oscillant à un degré de liberté . . . . . . . . . . . . . . . . . . . . . 33
4.2.2 Système à degré de liberté multiple . . . . . . . . . . . . . . . . . . . . . . 35
4.3 Chained’oscillateurs ................................... 38
II Ondes 39
5 Une approche
du phénomène de propagation 40
5.1 Le phénomène de propagation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
5.1.1 Généralisation................................... 40
5.1.2 Les différents types d’ondes . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
5.2 Ondes dans la chaine
d’oscillateurs........................................ 42
5.2.1 Équation de propagation dans la chaine d’oscillateurs . . . . . . . . . . . . 42
5.2.2 Solutions harmoniques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
5.2.3 Onde monochromatique progressive . . . . . . . . . . . . . . . . . . . . . 45
5.2.4 Longueur d’onde, vecteur d’onde . . . . . . . . . . . . . . . . . . . . . . . 45
5.2.5 Approximation des milieux continus . . . . . . . . . . . . . . . . . . . . . 46
5.3 Équations de propagation
ded’Alembert....................................... 47
5.3.1 Cordevibrante .................................. 48
5.3.2 Lignes de transmission . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
5.4 Solution de l’équation
depropagation ...................................... 51
5.4.1 Solutions harmoniques
de l’équation de d’Alembert . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
5.4.2 Caracteristiques des ondes planes progressives monochromatiques . . . . 53
5.5 Ondesstationnaires.................................... 54
5.5.1 Modes de vibration d’une corde fixée aux extrémités . . . . . . . . . . . . 55
III EXERCICES 57
6 Exercices 58
6.1 Associationsderessorts ................................. 58
6.2 RessortsetPoulies .................................... 58
6.3 Étude d’un oscillateur
à l’aide de son portrait de phase . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
6.4 Problème ......................................... 60
6.5 Etude de la résonance( TP 3èmeséance)......................... 62
6.6 Modélisation d’un amortisseur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
6.7 Sismographe (Devoir libre) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
6.8 Couplagede3ressorts .................................. 64
6.9 Oscillateurscouplés.................................... 64
6.10 Couplage de pendules simples identiques . . . . . . . . . . . . . . . . . . . . . . . 66
6.11 couplage ressort-pendule (1) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
6.12 Couplage ressort-barre (1) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
6.13 Couplage ressort-barre (2)
(Devoirlibre) ....................................... 68
6.14 Couplage ressort-barre (2) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
Physique des vibrations 3Université Ibn Tofail

TABLE DES MATIÈRES TABLE DES MATIÈRES
6.15Propagationd’onde.................................... 69
Physique des vibrations 4Université Ibn Tofail
 6
6
 7
7
 8
8
 9
9
 10
10
 11
11
 12
12
 13
13
 14
14
 15
15
 16
16
 17
17
 18
18
 19
19
 20
20
 21
21
 22
22
 23
23
 24
24
 25
25
 26
26
 27
27
 28
28
 29
29
 30
30
 31
31
 32
32
 33
33
 34
34
 35
35
 36
36
 37
37
 38
38
 39
39
 40
40
 41
41
 42
42
 43
43
 44
44
 45
45
 46
46
 47
47
 48
48
 49
49
 50
50
 51
51
 52
52
 53
53
 54
54
 55
55
 56
56
 57
57
 58
58
 59
59
 60
60
 61
61
 62
62
 63
63
 64
64
 65
65
 66
66
 67
67
 68
68
 69
69
 70
70
 71
71
 72
72
1
/
72
100%










