3g3 C Triangle rectangle et trigonométrie Cosinus, sinus, tangente d

3g3 C Triangle rectangle et trigonométrie
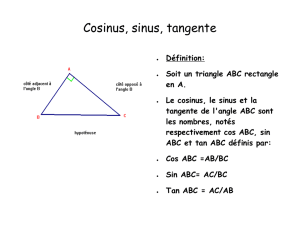
Cosinus, sinus, tangente d'un angle aigu
1.1 Définitions
A connaître
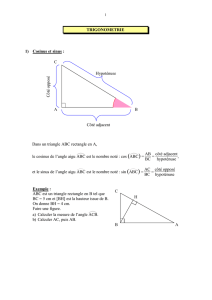
Dans un triangle rectangle,
le cosinus d'un angle aigu est le
quotient de la longueur du côté
adjacent à cet angle par la
longueur de l'hypoténuse.
le sinus d'un angle aigu est le
quotient de la longueur du côté
opposé à cet angle par la
longueur de l'hypoténuse.
la tangente d'un angle aigu est le
quotient de la longueur du côté
opposé à cet angle par la
longueur du côté adjacent à cet
angle.
1.2 Exemples
Exemple : Le triangle COR est rectangle en R.
Les formules donnant le cosinus et le sinus de l'angle
^
COR
puis la formule donnant la tangente de l'angle
^
OCR
sont :
Cos
^
COR
=
côté Adjacent à
^
COR
Hypoténuse
cos
COR
=
RO
CO
Sin
^
COR
=
côté Opposé à
^
COR
Hypoténuse
sin
^
COR
=
RC
CO
Tan
OCR
=
côté Opposé à OCR
côté Adjacent à OCR
tan
OCR
=
RO
RC
Remarques :
Le cosinus et le sinus d'un angle aigu sont toujours compris entre 0 et 1.
La tangente d'un angle aigu est un nombre strictement positif.
Moyen mnémotechnique
Si on désigne par :
•C le cosinus d'un angle aigu ;
•S le sinus d'un angle aigu ;
•T la tangente d'un angle aigu ;
•O la longueur du côté opposé ;
•A la longueur du côté adjacent ;
•H la longueur de l'hypoténuse ;
alors on peut écrire :
C =
A
H
; S =
O
H
; T =
O
A
On obtient alors un moyen mnémotechnique pour se rappeler facilement des trois définitions :
CAHSOHTOA*
* On peut prononcer « CASSE-TOI »
R
C
O
hypoténuse
côté
adjacent
à l'angle
^
COR
R
C
O
hypoténuse
côté
opposé
à
^
COR
R
C
O
côté
opposé
à l'angle
côté
adjacent
à
^
OCR
^
OCR
1

Relations trigonométriques
2.1 Relation entre cosinus, sinus et tangente
Soit ABC un triangle rectangle en A.
cos
^
ABC
=
AB
BC
sin
^
ABC
=
AC
BC
tan
^
ABC
=
AC
AB
sin
^
ABC
cos
^
ABC
=
AC
BC
AB
BC
sin
^
ABC
cos
^
ABC
=
AC
BC
×
BC
AB
sin
^
ABC
cos
^
ABC
=
AC
AB
sin
^
ABC
cos
^
ABC
= tan
^
ABC
2.2 Relation entre cosinus et sinus d'un angle aigu
Soit ABC un triangle rectangle en A.
cos
^
ABC
=
AB
BC
sin
^
ABC
=
AC
BC
( cos
^
ABC )
2
+
( sin
^
ABC )
2
=
(
AB
BC
)
2
+
(
AC
BC
)
2
( cos
^
ABC )
2
+
( sin
^
ABC )
2
=
(
AB2+AC2
BC2
)
or d'après le théorème de Pythagore AB2 + AC2 = BC2
donc
( cos
^
ABC )
2
+
( sin
^
ABC )
2
=
BC2
BC2
( cos
^
ABC )
2
+
( sin
^
ABC )
2
= 1
A connaître
Pour tout angle aigu
^
A
:
( cos
^
A )
2
+
( sin
^
A )
2
= 1
et tan
^
A
=
sin
^
A
cos
^
A
Remarque : La première formule peut aussi s'écrire cos2
^
A
 sin2
^
A
= 1.
2