TRIGONOMÉTRIE

~ 1 ~
C. Lainé
TRIGONOMÉTRIE
1. Cosinus, sinus, tangente d’un angle aigu
Remarque : Pour mémoriser ces formules, on peut dire CAH SOH TOA (« casse-toi ! »
2. Utilisation de la calculatrice
• Avant d’utiliser les touches cos , sin et tan d’une calculatrice, il est nécessaire de
mettre celle-ci en mode degrés ( voir le mode d’emploi de votre calculatrice ).
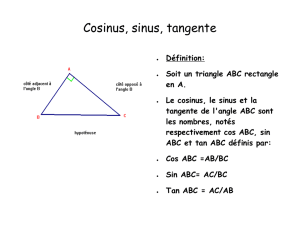
Soit
ABC
un triangle rectangle en
A
.
Le cosinus, le sinus et la tangente de l’angle aigu
ABC
sont les nombres,
notés respectivement
(
)
cos
ABC
,
(
)
sin
ABC
et
(
)
tan
ABC
définis par :
( )
côté djacent à
os ypoténu
A
eHs
C
ABC
ABC =
;
( )
côté pposé à
in ypoténuseH
O
S
ABC
ABC =
;
( )
côté pposé à
an côté djacent TA à
O
ABC
ABC
ABC
=
.
Objectifs :
• Connaître et utiliser les relations entre le cosinus, le sinus ou la tangente
d’un angle aigu et les longueurs de deux des côtés d’un triangle rectangle.
• Déterminer, à l’aide de la calculatrice, des valeurs approchées :
- du sinus, du cosinus et de la tangente d’un angle aigu donné ;
- de l’angle aigu dont on connaît le cosinus, le sinus ou la tangente.

~ 2 ~
C. Lainé
CASIO FX
-
92
TI
-
COLLÈGE PLUS
D
doit être affiché
en haut de l’écran.
DEG
doit être affiché
en haut à droite de l’écran.
Mettre la calculatrice en mode « Degré » si elle ne l’est pas
Détermination de
(
)
sin 52
°
Détermination de l’angle
θ
tel que
(
)
tan 4
=
θ
3. Relations fondamentales
Remarque : La première formule peut également s’écrire
(
)
(
)
2 2
cos sin 1
A A
+ =
.
Exemple : Calculer la valeur exacte de
(
)
sin A
et de
(
)
tan A
sachant que
(
)
tan A
est un
angle aigu tel que
(
)
cos A = 0,8
.
• On sait que
(
)
(
)
2 2
cos sin 1
A A
+ =
, alors
(
)
(
)
2 2 2
sin 1 cos 1 0,8 1 0, 64 0,36
A A= − = − = − =
.
D’où
(
)
0,36=
sin 0,6
=A
.
•
( )
(
)
( )
sin 0,6
cos 0,8
A
A
= =
tan 0,75
=A
.
Pour tout angle aigu
A
,
(
)
(
)
(
)
(
)
2 2
cos sin 1
+ =
A A
et
( )
(
)
( )
sin
tan
cos
=
A
A
A
.