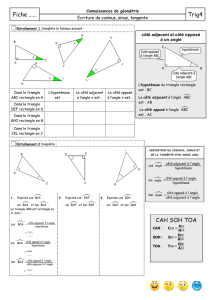
LES RELATIONS TRIGONOMETRIQUES

3
ème
LES RELATIONS TRIGONOMETRIQUES
Trigo1
ABC est un triangle rectangle en A.
a) Ecris une formule faisant intervenir l’angle ABC, AB et AC.
b) Ecris une formule faisant intervenir l’angle ABC, AB et BC.
tan ABC AC
AB
=
a) [ ] est le côté adjacent à l’angle et [ ] son côté opposé, donc j’utilise la tangente : AB ABC AC
b) [ ] est le côté adjacent à l’angle et [ ] est l’hypoténuse, donc j’utilise le cosinus : AB ABC BC
cos ABC AB
BC
=
(”côté opposé sur côté adjacent”)
(”côté opposé sur hypoténuse”)
Dessine un triangle TOP rectangle en P.
a) Exprime cos OTP, sin OTP et tan OTP à
l’aide des côtés de ce triangle.
b) Fais la même chose avec l’angle TOP.
Recopie et complète :
Enoncé :
Dessine un triangle KLM rectangle en K.
Exprime sin KLM, cos KLM et tan KLM à l’aide
des côtés de ce triangle.
Solution :
sin KLM
=
…
LM
cos KLM
=
…
…
tan KLM
=
KM
…
ABC est un triangle rectangle en A.
a) Ecris les rapports correspondant à sin ABC,
cos ABC et tan ABC.
b) Ecris les rapports correspondant à sin ACB,
cos ACB et tan ACB.
Sur la figure ci-dessous, écris
trois rapports égaux à sin CAD :
Recopie et complète en utilisant la
calculatrice (résultats arrondis au dixième) :
a) x = 50°, donc cos x ≈ …
b) x = 72°, donc sin x ≈ …
c ) cos x = 0,7, donc x ≈ …
d) tan x = 5
3, donc
x ≈ …
e) sin x = 0,5, donc x ≈ ...
A
B
C
A
côté opposé à A
hypoténuse
côté adjacent à A
L
K
M
A
B
C
D
E
A
B
C
Dans un triangle rectangle, on définit les relations trigonométriques suivantes :
cos A = « côté adjacent »
« hypoténuse » = AC AB
sin A = « côté opposé »
« hypoténuse » = BC AB
tan A = « côté opposé »
« côté adjacent » = BC AC
INFO
INFO
Précise à
chaque fois
dans quel
triangle tu te
places !