Nouveaux programmes de première Probabilités et statistiques

Nouveaux programmes de première – Probabilités et statistiques Octobre 2011
Nouveaux programmes de première
Probabilités et statistiques
I. Statistiques descriptives
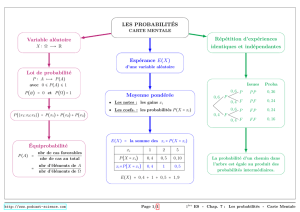
II. Probabilités
- Variables aléatoires discrètes
- Arbres
- Loi géométrique tronquée
- Loi binomiale
III. Échantillonnage
Ressources en ligne

Nouveaux programmes de première – Probabilités et statistiques Octobre 2011
I. Statistiques descriptives, analyse de données
Seconde
Moyenne
Médiane, quartiles
Représentations graphiques :
histogramme,
nuage de points,
courbe de fréquences cumulées
Première
Variance,
écart-type
Diagramme en boîte
(sauf STI2D)
Objectif
comparaison de séries statistiques
Objectif
synthétiser,représenter une série statistique

Nouveaux programmes de première – Probabilités et statistiques Octobre 2011
II. Probabilités
II-1. De la seconde à la première
Seconde Première
Variable aléatoire discrète
Arbres pondérés
pas de probabilités conditionnelles
Loi géométrique tronquée,
loi binomiale
Objectif
étudier un grand nombre
d'expériences identiques et indépendantes
Objectif
modéliser une expérience
aléatoire dans le cadre
de l'équiprobabilité
Probabilité d'un événement
en situation d'équiprobabilité
Arbres et tableaux
pA∪B pA∩B= pA pB

Nouveaux programmes de première – Probabilités et statistiques Octobre 2011
II-2. Variable aléatoire discrète
Loi d'une variable aléatoire discrète
(ES/L et S)
Espérance
Variance, écart-type
(en S)
Démonstration (en S) :
E(aX+ b) = aE(X)+b
Démonstration :
V(aX)= a² V(X)
Lien avec les statistiques :
Interpréter l’espérance comme
valeur moyenne dans le cas
d’un grand
nombre de répétitions.
(extrait doc. accompagnement, p. 6)
Lancer d'un dé à 6 faces
Numéro de la face 1 2, 3, 4 5, 6
Valeur de X 1 2 4
p(X=xi) 1/6 3/6 2/6

Nouveaux programmes de première – Probabilités et statistiques Octobre 2011
II-3. Arbres pondérés, répétitions indépendantes
Arbres
Objectif :
passer de l'arbre des issues à l'arbre pondéré
(doc. accompagnement p. 8 à 11)
Répétitions d'expériences indépendantes
Exemples :
tirer une boule puis lancer un dé
tirer une boule puis une carte
Répétition d'expériences identiques et indépendantes
Objectif : mettre en place la notion d'expériences identiques et indépendantes à plusieurs
issues ; réinvestir les arbres pondérés
Exemple : on fait tourner plusieurs fois une roue divisée en secteurs de couleurs différentes