fonction exponentielle 4eme sc techniques

Dans tous les exercices le plan est rapporté à un repère orthonormé
Exercice 1
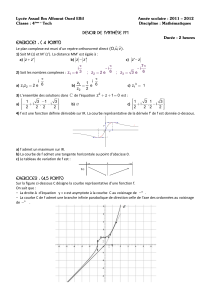
On a représenté ci-
dessous la courbe représentative (C) d’une fonction f définie, continue et
On sait que la courbe (C) admet :
• Une asymptote d’équation
)j , O( au voisinage de
∞−
•
Seulement deux tangentes horizontales
En utilisant le graphique :
1) Déterminer )x(flim
x+∞→
, )x(flim
x−∞→
et
2) Déterminer, suivant la valeur du paramètre réel m, le nombre de solutions de l’équation
Exercice 2
Soit f la fonction définie sur IR par
x
(f
1) Dresser le tableau de variation de f.
a) Justifier que la restriction g de f à l’intervalle
b) Montrer que l’équation 0)x(f =
c) Vérifier que 5,11 <α<
2) a) Calculer
x)x(f
lim
x−∞→
. Interpréter graphiquement le résultat .
b) Etudier la position relative de la courbe (
c) Tracer ( ζ ) et
∆
.
3) On note
1
g
−
la fonction réciproque de g et (
4)
Vérifier que la fonction F définie par
Exercice 3
Soit la fonction f définie sur IR par :
x
(f
1) a) Montrer que f est dérivable sur IR et que pour tout
b) Etudier les variations de f.
c) Vérifier que pour tout
IRx∈
,
(
f
Kooli Mohamed Hechmi
FONCTION EXPONENTIELLE 4
Dans tous les exercices le plan est rapporté à un repère orthonormé
dessous la courbe représentative (C) d’une fonction f définie, continue et
0y = au voisinage de ∞+
et une branche parabolique de direction
.
Seulement deux tangentes horizontales
; l’une au point O et l’autre au point
x)x(f
lim
x−∞→
.
2) Déterminer, suivant la valeur du paramètre réel m, le nombre de solutions de l’équation
xx
xee1)
x
−+= . On note (
ζ ) sa courbe
représentative.
a) Justifier que la restriction g de f à l’intervalle
[ [
∞+ , 0
réalise une bijection de
admet dans IR, une solution unique α .
. Interpréter graphiquement le résultat .
b) Etudier la position relative de la courbe (
ζ ) et la droite
∆
d’équation
xy =
.
la fonction réciproque de g et (
ζ′
) sa courbe représentative. Tracer (
Vérifier que la fonction F définie par
x
e)x2(x)x(F −+=
est une primitive de f sur IR.
)e1ln(
2
1
)
x
x−
+= . On désigne par ( ζ
) sa courbe représentative.
1) a) Montrer que f est dérivable sur IR et que pour tout
IRx∈
,
x
e1 1
2
1
)x(f + −=
′
)e1ln(
2
1
x
2
1
)x
(
x
++−= .
Kooli Mohamed Hechmi
http://mathematiques.kooli.me/
FONCTION EXPONENTIELLE 4
eme
Sc Tech
niques
Dans tous les exercices le plan est rapporté à un repère orthonormé
)j,i,O( rr
dessous la courbe représentative (C) d’une fonction f définie, continue et
dérivable sur IR.
et une branche parabolique de direction
; l’une au point O et l’autre au point
) 4e , 2 (A
-2
.
2) Déterminer, suivant la valeur du paramètre réel m, le nombre de solutions de l’équation
m)x(f = .
représentative.
réalise une bijection de
[ [
∞+ , 0 sur
] ]
2 , ∞− .
) sa courbe représentative. Tracer (
ζ′ ).
est une primitive de f sur IR.
) sa courbe représentative.
.
http://mathematiques.kooli.me/
niques

d) En déduire que la droite y:
−
=∆
Etudier la position relative de ( ζ ) et
∆
e) Tracer ( ζ ) et
∆
.
2) a) Montrer que l’équation x)x(f =
b) Vérifier que 10 <α< .
3) a) Montrer que pour tout 0x ≥ ,
(
f′
b) En déduire que tout 0x ≥ ,
−
)x(f
Exercice 4
1) La courbe ( Γ ) ci-
dessous est celle d’une fonction g définie, continue et dérivable sur IR.
On sait que :
• La droite d’équation
1
y−=
• La courbe ( Γ
) admet une seule tangente horizontale.
• La courbe ( Γ
) coupe l’axe des abscisses
En utilisant le graphique :
a) Déterminer )0(g et )0(g′ .
b) Déterminer le signe de g sur IR.
2) La fonction g est définie sur IR par
a) Exprimer )0(g et )0(g′
en fonction de
b) Déduire, en utilisant 1)a), que pour tout réel x,
Dans la suite de l’exercice, on considère la fonction f définie sur
On désigne par ( ζ
) sa courbe représentative.
3) a) Calculer )x(flim
x−∞→
, )x(flim
0x
−
→
et
lim
x
b) Calculer )x(flim
x+∞→
c) Justifier que la courbe ( ζ
) admet une branche parabolique de direction
4) a) Vérifier que pour tout
∗
∈ IRx ,
f
b) Dresser le tableau de variation de f.
c) Montrer que 1x 1 )x(f
0
0−
=.
d) Tracer ( ζ ). ( On prendra 2,1x
0
= ).
x
2
1
−
est une asymptote à ( ζ ) en
∞−
.
.
admet dans IR une solution unique α .
4
1
)x
(
≤ .
α−≤α
−
x
4
1
.
dessous est celle d’une fonction g définie, continue et dérivable sur IR.
1
est une asymptote à ( Γ ) au voisinage de (
−
) admet une seule tangente horizontale.
) coupe l’axe des abscisses
)i , O( en un unique point
0
x .
2) La fonction g est définie sur IR par
1e)x()x(g
x
−β+α=
où α et β
sont deux réels.
en fonction de
α et β .
b) Déduire, en utilisant 1)a), que pour tout réel x,
1e)1x()x(g
x
−−=
Dans la suite de l’exercice, on considère la fonction f définie sur
∗
IR par
x
e
)x(f
x
=
) sa courbe représentative.
)x(f
lim
0
x
+
→
.Interpréter graphiquement le résultat .
) admet une branche parabolique de direction
)j , O(
au voisinage de
2
x)x(g
)x(
f
=
′
.
b) Dresser le tableau de variation de f.
Kooli Mohamed Hechmi
http://mathematiques.kooli.me/
dessous est celle d’une fonction g définie, continue et dérivable sur IR.
∞
−
).
sont deux réels.
x
1+.
.Interpréter graphiquement le résultat .
au voisinage de
∞+
http://mathematiques.kooli.me/

Exercice 5
Soit la fonction f définie sur IR par :
x
e)x1()x(f
−
+=
. On désigne par (
ζ
) la courbe représentative de f.
1) a) Calculer )x(flim
x−∞→
et )x(flim
x+∞→
.
b) Montrer que pour tout réel x ,
x
xe)x(f
−
−=
′
.
c) Dresser le tableau de variation de f.
2) a) Calculer
x
)x(f
lim
x−∞→
. Interpréter graphiquement le résultat obtenu.
b) Tracer la courbe (
ζ
).
3) Soit la fonction définie sur IR par = − + 2 , montrer que est une primitive de f sur IR.
Exercice 6
On considère la fonction f définie sur IR par :
>= ≤+−= 0 xsi lnx x -xf(x)
0 xsie1x)x(f
x
Soit (C) sa courbe représentative ( unité graphique 2cm )
1) a) Montrer que f est continue en 0
b) Montrer que f est dérivable à gauche en 0 est que le nombre dérivé à gauche en 0 est 2
c) Etudier la dérivabilité de f à droite en 0
2) a) Etudier les variations de f sur
]
]
0 , -
∞
puis sur
]
[
∞
+
, 0
b) En déduire le tableau de variation de f sur IR
3) a) Montrer que la droite 1xy:
−
=
∆
est une asymptote à (C) au voisinage de
∞
−
b) Préciser pour
0x
≤
, la position de (C) par rapport à
∆
c) Préciser pour
0x
>
, la position de (C) par rapport à xy:
=
∆
′
d) Déterminer une équation cartésienne de la tangente T à la courbe (C) au point 0) , e(A
4) Tracer
∆
,
∆
′
, T et (C)
5) Soit g la restriction de f à l’intervalle
[
[
∞
+
, 1
a) Montrer que g admet une fonction réciproque
1
g
−
définie sur un intervalle J que l’on précisera. On
désigne par )C(
′
la courbe représentative de
1
g
−
b) Vérifier que la droite T définie dans A)3)d) est tangente à la courbe )C(
′
au point e) , 0(B
c) Tracer )C(
′
Exercice 7
Soit f la fonction définie sur
]
[
1 , 0 par : 
−
=x1 x ln)x(f
1) a) Dresser le tableau de variation de f
b) Montrer que f possède une fonction réciproque définie sur IR par
x
x
e
1
e
)x(g
+
=
2) On désigne par (C) la courbe de g ( Unité graphique 4cm )
a) Montrer que (C) est symétrique par rapport au point 
2
1
, 0I
b) Calculer )x(g
′
pour tout x
∈
IR et dresser le tableau de variation de g
c) Vérifier que I
∈
(C) et montrer que la tangente T à (C) en I a pour équation :
2
1
x
4
1
y +=
d) Montrer que pour tout x
∈
IR
4
1
)x(g ≤
′
Kooli Mohamed Hechmi http://mathematiques.kooli.me/

3) Soit h la fonction définie sur IR par
a) Etudier le sens de variation de h
b) Calculer )0(h et en dédui
re le signe de
4) Etudier la position de (C) et T
5) a) Montrer que l’équation x)x(f =
b) Tracer (C) et T et la courbe (C’) de f
6) Soit G la primitive de g tel que
0
(G
a) Montrer que pour tout x ∈ IR
(
F
b) Dresser le tableau de variation de F
c) Montrer que la courbe Γ
de F est asymptote à la droite
d) Préciser la position de Γ
par rappo
Exercice 8
On a représente ci-
dessous dans un repère orthonormé la courbe (C) d’une fonction f définie, continue,
dérivable et strictement décroissante sur
On sait que la courbe (C) :
* admet l’axe des abscisses comme asymptote au voisinage de
* atteint son maximum au point d’abscisse 0.
1) Par lecture graphique :
a) Déterminer )0(f )x(flim
x+∞→
et
0
(f
d
′
b) Montrer que f est une bijection de
2) Tracer la courbe )C( ′
de la fonction
On note β l’abscisse du p
oint d’intersection des deux courbes (C) et
3) On sait que la fonction f est définie sur
4)
En utilisant 1) a) montrer que pour tout x de
Exercice 9
A) Soit g la fonction définie sur IR par
1) a) Etudier les variations de g
b) Déduire que
IRx ∈∀
on a : )x(g
B) Soit f la fonction définie sur IR par
:
1) Montrer que +∞=
+∞→
)x(f
lim
x
et que
2) a) Montrer que la droite xy: =∆
est une asymptote oblique à la courbe (C) au voisinage de
Kooli Mohamed Hechmi
3) Soit h la fonction définie sur IR par
2
1
x
4
1
)x(g)x(h −−=
a) Etudier le sens de variation de h
re le signe de
)x(h sur IR
possède une seule solution α et que 5,0
α
<
b) Tracer (C) et T et la courbe (C’) de f
2ln)
0
= et
[ ]
)x(glnx:F a
)x(Gx)x
(
−=
b) Dresser le tableau de variation de F
de F est asymptote à la droite
xy:D =
au voisinage de
par rappo
rt à D. Tracer Γ
dessous dans un repère orthonormé la courbe (C) d’une fonction f définie, continue,
dérivable et strictement décroissante sur
[ [
, 0 ∞+ .
* admet l’axe des abscisses comme asymptote au voisinage de
∞+
* atteint son maximum au point d’abscisse 0.
)
0
(nombre dérivé à droite en 0)
b) Montrer que f est une bijection de
[ [
, 0 ∞+
sur un intervalle J que l’on déterminera.
de la fonction
1
f
−
réciproque de f.
oint d’intersection des deux courbes (C) et
)C( ′
3) On sait que la fonction f est définie sur
[ [
, 0 ∞+ par
x2
e)bax()x(f
−
+=
.où a et b
En utilisant 1) a) montrer que pour tout x de
[ [
, 0 ∞+ ;
x2
e)1x2()x(f
−
+=
.
:
1xe)x(g
x
−−=
0≥
:
xe2xe)x(f
xx
+−=
et soit (C) sa courbe représentative
et que
+∞=
+∞→
x)x(f
lim
x
. Interpréter les résultats
est une asymptote oblique à la courbe (C) au voisinage de
Kooli Mohamed Hechmi
http://mathematiques.kooli.me/
75,0<
α
au voisinage de
∞−
dessous dans un repère orthonormé la courbe (C) d’une fonction f définie, continue,
sur un intervalle J que l’on déterminera.
.où a et b
sont deux réels.
et soit (C) sa courbe représentative
est une asymptote oblique à la courbe (C) au voisinage de
∞−
http://mathematiques.kooli.me/

b) Préciser la position de (C) par rapport à la droite
∆
3) a) Montrer que pour tout réel x on a :
)x(ge)x(f
x
−=
′
b) En déduire que la fonction f est strictement croissante sur IR
c) Dresser le tableau de variation de f
4) Tracer la courbe (C) en précisant la tangente au point d’abscisse 0
Exercice 10
Soit f la fonction définie sur IR par
1
e
e2
)x(f
x
x
+
=
et soit (C) sa courbe représentative ( Unité 2cm )
1) a) Calculer
)x(f
lim
x+∞→
et )x(f
lim
x−∞→
b) Montrer que
IR
x
∈
∀
on a :
2x
x
)1e( e2
)x(f + =
′
c) Dresser le tableau de variation de f
2) a) Montrer que le point
I
de (C) d’abscisse 0 est un centre de symétrie de (C)
b) Donner une équation cartésienne de la tangente T à (C) au point I
3) On pose pour tout
IR
x
∈
, x)x(f)x(g
−
=
a) Etudier les variations de g
b) Montrer que l’équation 0)x(g
=
admet dans IR une unique solution
α
et que 7,16,1
<
α
<
c) Etudier alors les position relatives de (C) et la droite xy:
=
∆
4) Construire (C) , T et
∆
5) a) Montrer que f réalise une bijection de IR sur
]
[
2 , 0
b) Calculer
)x(f
1−
∈
∀
x
]
[
2 , 0
c) Construire la courbe (C’) représentative de
1
f
−
dans le même repère
Exercice 11
Soit f la fonction définie sur IR par :
x
e
1
1
x)x(f
+
−= et soit (C) sa courbe représentative
1) a) Vérifier que pour tout réel x on a : 0)x(f
>
′
b) Dresser le tableau de variation de f
2) a) Montrer que la droite xy:
1
=
∆
et la droite 1xy:
2
−
=
∆
sont asymptotes à la courbe (C)
b) Préciser les positions de (C) par rapport à
1
∆
et
2
∆
3) a) Montrer que f réalise une bijection de IR sur IR et en déduire que l’équation 0)x(f
=
admet dans IR
une unique solution
α
et que 14,0
<
α
<
b) Vérifier que
α
=+
α
1
1e
4) a) Montrer que 
−2
1
,0I est un point d’inflexion de la courbe (C)
b) Donner une équation cartésienne de la tangente T à la courbe (C) au point I
c) Montrer que la tangente T coupe l’axe des abscisses au point A d’abscisse 0,4
5) Tracer
1
∆
,
2
∆
, T et (C). (On prendra 45,0
≈
α
)
Exercice 12
Soit f la fonction définie sur IR par :
2e2e)x(f
xx2
+−=
et soit (C) sa courbe représentative
1) a) Calculer )x(f
lim
x−∞→
et )x(f
lim
x+∞→
b) Vérifier que
IR
x
∈
∀
on a :
)1e(e2)x(f
xx
−=
′
c) Dresser le tableau de variation de f
Kooli Mohamed Hechmi http://mathematiques.kooli.me/